3. Convex function

Convex function

$f:\R^n \to \R$ is convex if $\text{dom }f$ is a convex set and

$$f(\theta x + (1 - \theta)y ) \le \theta f(x) + (1-\theta)f(y)$$

for all $x, y\in \text{dom }f, 0 \le\theta \le 1$

$f$ is strictly convex if $\text{dom }f$ is convex and

$$f(\theta x + (1 - \theta)y ) < \theta f(x) + (1-\theta)f(y)$$

for all $x, y\in \text{dom }f, 0 \le\theta \le 1$

Examples

affine functions are convex and concave; all norms are convex

Examples on $\R$

1. affine : $a x + b$ on $\R$, for any $a, b\in \R$

2. exponential : $e^{ax}$, for any $a\in \R$

3. powers : $x^\alpha$ on $\R_{++}$, for $\alpha \ge 1$ or $\alpha \le 0$

4. powers of absolute value : $|x|^p$ on $\R$, for $p\ge1$

5. negative entropy : $-x\log x$ on $\R_{++}$

Examples on $\R^n$

• affine function : $f(x) = a^Tx + b$

• norms : $\|x\|_p = (\sum_{i = 1}^n|x_i|^p)^{1/p}$ for $p\ge 1$; $\|x\|_\infty = \max_k |x_k|$
  • Proof

    $$\begin{aligned}\|\theta x + (1-\theta)y\| &\le \|\theta x \| + \|(1-\theta) y\| \\ &\le\theta\|x\| + (1-\theta)\|y\|\end{aligned}$$

Examples on $\R^{m\times n}$

• affine function

  $$f(X) = \text{tr}(A^TX) + b = \sum_{i = 1}^m \sum_{j = 1}^n A_{ij}X_{ij} + b$$

  💡

  Actually, $\text{tr}(A^TB) = \langle A, B\rangle_F$ is a generalized inner-product of two matrices

  Frobenius inner product

  In mathematics, the Frobenius inner product is a binary operation that takes two matrices and returns a scalar. It is often denoted &#x27E8; A , B &#x27E9; F {\displaystyle \langle \mathbf {A} ,\mathbf {B} \rangle _{\mathrm {F} }} . The operation is a component-wise inner product of two matrices as though they are vectors, and satisfies the axioms for an inner product. The two matrices must have the same dimension - same number of rows and columns, but are not restricted to be square matrices.

  https://en.wikipedia.org/wiki/Frobenius_inner_product

• spectral (maximum singular value) norm

  $$f(X) = \|X\|_2 = \sigma_{\max}(X) = (\lambda_{\max}(X^TX))^{1/2}$$

  💡

  The spectral norm of a matrix $A$ is the largest singular value of $A$. It is a special case of p-norm when p is 2.

  Matrix norm

  In mathematics, we can define norms for the elements of a vector space. When the vector space in question consists of matrices, these are called matrix norms.

  https://en.wikipedia.org/wiki/Matrix_norm

Restriction of a convex function to a line

$f : \R^n \to \R$ is convex if and only if the function $g :\R \to \R$

$$g(t) = f(x + tv), \quad \text{dom g} = \{t|\; x + tv \in \text{dom }f\}$$

is convex in t for any $x\in \text{dom f}, v\in \R^n$

We can check convexity of $f$ by checking convexity of functions of one variable

💡

We can interpret this as a fixed direction and starting point to check the convexity of the given function

Example

$f:S^n \to \R$ with $f(X) = \log \det X, \text{dom }f = S_{++}^n$

$$\begin{aligned}g(t) = \log \det(X + tV) &= \log \det X + \log\det (I + tX^{-1/2}VX^{-1/2}) \\ &= \log\det X + \sum_{i = 1}^n \log(1 + t\lambda_i)\end{aligned}$$

where $\lambda_i$ are the eigenvalues of $X^{-1/2}VX^{-1/2}$

$g$ is concave in $t$ (for any choice of $X\succ 0, V$); hence $f$ is concave.

Note

$$\begin{aligned}\log \det(X + tV) &= \log \det (X^{1/2}X^{1/2} + tX^{1/2}X^{-1/2}VX^{-1/2}X^{1/2})\\ &= \log\det(X^{1/2}(I + tX^{-1/2}VX^{-1/2})X^{1/2}) \\ &= \log\det(X(I + tX^{-1/2}VX^{-1/2})) \\ &= \log \det X + \log\det(I + tX^{-1/2}VX^{-1/2})\end{aligned}$$

Extended-value extension

It is often convenient to extend a convex function to all of $\R^n$ by defining its value to be $\infty$ outside its domain. If $f$ is convex we define its extended-value extension $\tilde f$ of $f$ is

$$\tilde f(x) = \begin{cases}f(x) \quad x\in \text{dom }f \\ \infty \quad x\notin \text{dom }f\end{cases}$$

The extension can simplify notation, since we don’t need to explicitly describe the domain.

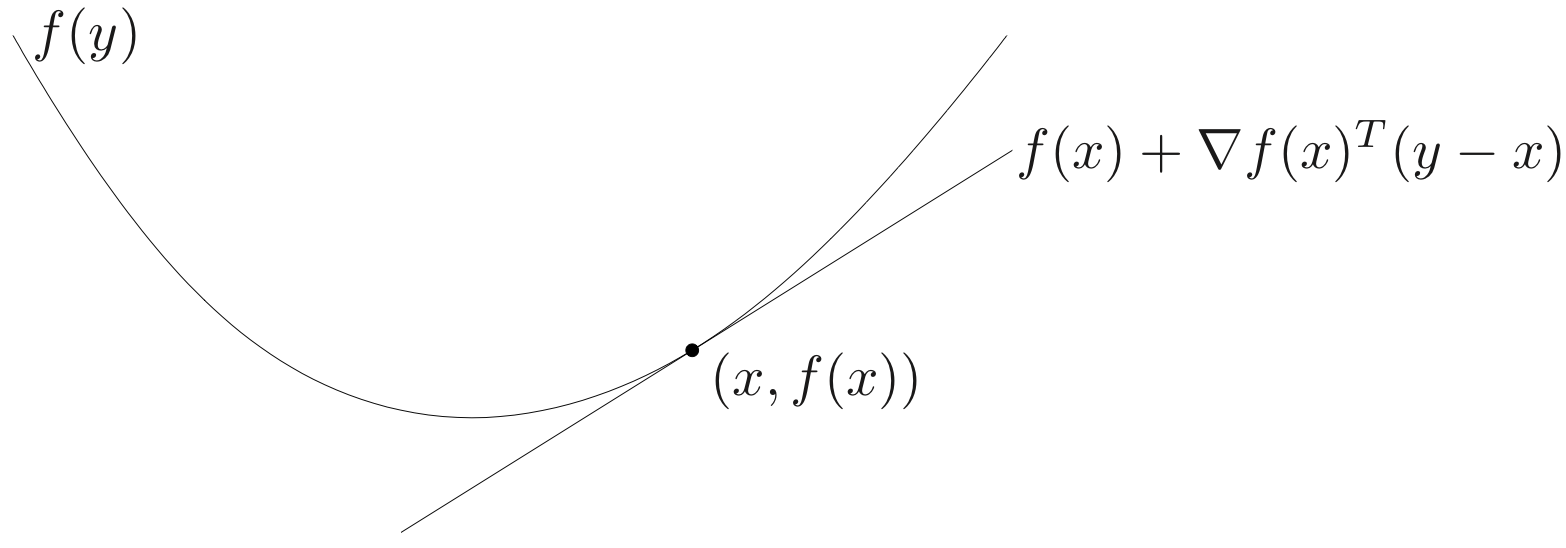
First-order condition

$f$ is differentiable if $\text{dom }f$ is open and the gradient

$$\nabla f(x) = \bigg (\frac{\partial f(x)}{\partial x_1}, \frac{\partial f(x)}{\partial x_2}, \cdots, \frac{\partial f(x)}{\partial x_n}\bigg)^T$$

exists at each $x\in \text{dom }f$

1st-order condition : differentiable $f$ with convex domain is convex if and only if

$$f(y) \ge f(x) + \nabla f(x)^T(y- x), \forall x, y\in \text{dom }f$$

Second-order conditions

$f$ is twice differentiable if $\text{dom }f$ is open and the Hessian $\nabla^2f(x) \in S^n$,

$$\nabla^2f(x)_{ij} = \frac{\partial^2f(x)}{\partial x_i\partial x_j}, \quad i, j = 1, \dots, n$$

or equivalently

$$\nabla^2f(x)_{ij} = H_x(i, j)$$

where $H_x$ is a hessian matrix at $x$.

2nd-order condition : for twice differentiable $f$ with convex domain

• $f$ is convex if and only if

  $$\nabla^2 f(x) \succeq0, \forall x\in \text{dom }f$$

• if $\nabla^2 f(x) \succ 0, \forall x\in \text{dom }f$, then $f$ is strictly convex.

Example

1. Quadratic function : $f(x) = \frac{1}{2}x^TPx + q^Tx + r$ (with $P\in S^n)$

   $$\nabla f(x) = Px + q, \quad \nabla^2f(x) = P$$

   convex if $P\succeq 0$

2. Least-squares objective : $f(x) = \|Ax -b \|_2^2$

   $$\nabla f(x) = 2A^T(Ax - b), \quad \nabla^2 f(x) = 2A^TA$$

   convex for any $A$ since $A^TA$ is always positive semi-definite.

3. quadratic-over-linear : $f(x,y) = x^2/y$

   $$\nabla^2f(x, y) = \frac{2}{y^3}\begin{bmatrix}y \\ -x\end{bmatrix}\begin{bmatrix}y \\ -x\end{bmatrix}^T \succeq0$$

   convex for $y>0$

4. log-sum-exp : $f(x) = \log\sum_{k = 1}^n \exp x_k$

   $$\nabla f(x) = (\exp x_1/\sum_{k = 1}^n\exp x_k, \exp x_2/\sum_{k = 1}^n\exp x_k, \cdots, \exp x_n/\sum_{k = 1}^n\exp x_k)^T$$

   Then,

   $$\nabla_{ii}^2 f(x) = \exp x_i/\sum_{k = 1}^n\exp x_k + \exp x_i * -\frac{\exp x_i}{(\sum_{k = 1}^n\exp x_k)^2} \\ \nabla_{ij}^2 f(x) = \exp x_i * -\frac{\exp x_j}{(\sum_{k = 1}^n\exp x_k)^2} (i \ne j)$$

   Therefore,

   $$\nabla^2 f(x) = \frac{1}{1^Tz}\text{diag}(z) - \frac{1}{(1^Tz)^2}zz^T \quad (z_k = \exp x_k)$$

   to show $\nabla^2 f(x)$ is positive semi-definite, we must verify that $v^T\nabla^2f(x) v\ge 0, \forall v$

   $$v^T\nabla^2f(x)v = \frac{(\sum_{k}z_kv_k^2)(\sum_{k}z_k) - (\sum_k v_kz_k)^2}{(\sum_k z_k)^2}$$

   By Cauchy-Schwarz inequality,

   $$(\sum_k v_kz_k)^2 \le (\sum_k z_kv_k^2)(\sum_k z_k)$$

   So, $v^T\nabla^2f(x)v\ge 0, \forall v$.

   Therefore, $\nabla^2f(x)$ is a positive semi-definite matrix.

   💡

   This function is a smooth approximation of a maximum since the maximum number nominate the value. In deep learning or machine learning perspective, we call this function as a softmax function.

5. geometric mean : $f(x) = (\prod_{k = 1}^n x_k)^{1/n}$ on $\R_{++}^n$ is concave

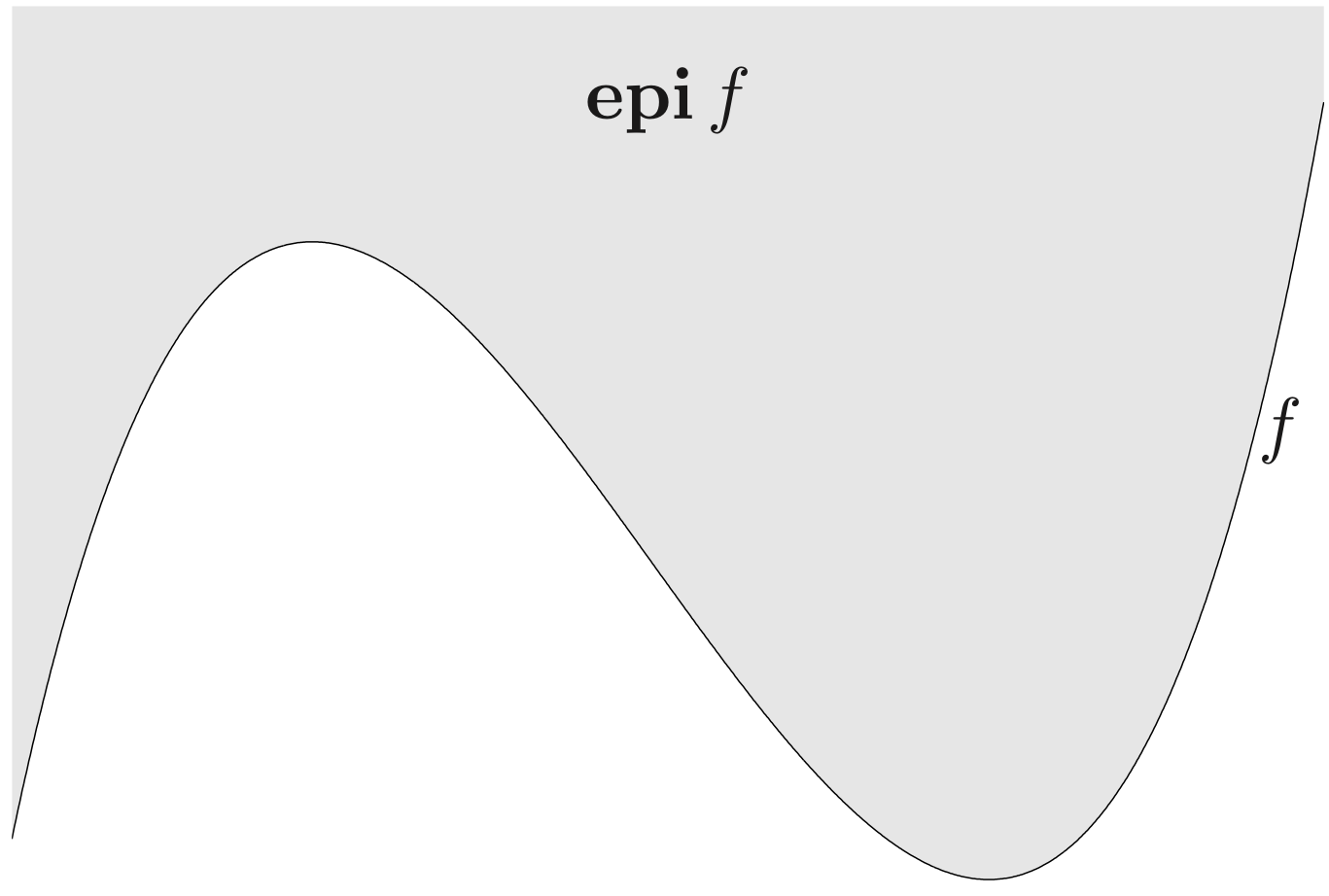
Epigraph and sublevel set

$\alpha$-sublevel set of $f:\R^n\to \R:$

$$C_\alpha = \{x\in \text{dom }f|\;f(x)\le \alpha\}$$

sublevel sets of convex functions are convex

epigraph of $f :\R^n\to \R$

$$\text{epi }f=\{(x, t)\in \R^{n + 1}|\; x\in \text{dom }f, f(x)\le t\}$$

💡

$f$ is convex if and only if $\text{epi }f$ is a convex set.

Jensen’s inequality

basic inequality : if $f$ is convex, then for $0\le\theta \le 1$

$$f(\theta x + (1 - \theta)y)\le \theta f(x) + (1-\theta)f(y)$$

💡

It actually extended to the finite sum to infinite sum. Therefore, this equality still holds if we integrate them. That’s why the following inequality holds.

extension : if $f$ is convex, then

$$f(E z) \le Ef(z)$$

for any random variable $z$

💡

The clarity of this result stems from the fundamental nature of abstract integration, which essentially involves the summation of infinitesimally small quantities.

Operations that preserve convexity

practical methods for establishing convexity of a function

1. by using definition

2. for twice differentiable functions, show $\nabla^2f(x)\succeq 0, \forall x$

3. show that $f$ is obtained from simple convex functions by operations that preserve convexity
   1. nonnegative weighted sum
   2. composition with affine function
   3. point-wise maximum and supremum
   4. minimization
   5. composition with scalar function
   6. vector composition
   7. perspective

Composition with affine function

$$f(Ax + b)$$

is convex if $f$ is convex

• Proof

  Given $x,y\in \text{dom }A, \theta \ge 0$

  $$\begin{aligned} f(\theta (Ax+b) + (1-\theta)(Ay + b)) &= f(A(\theta x + (1-\theta)y) + b) \\&\le \theta f(Ax + b) + (1-\theta)f(Ay + b)\end{aligned}$$

  Therefore $f(Ax + b)$ is a convex function.

Examples

1. log barrier for linear inequalities

   $$f(x) = -\sum_{i = 1}^m \log (b_i - a_i^Tx)$$

   where $\text{dom }f = \{x|a_i^Tx<b_i, i = 1, \dots, m\}$

   💡

   Since log is convex and it is composited by the affine function, it is also a convex function

2. any norm of affine function

   $$f(x) = \|Ax + b\|$$

   💡

   We already know that every norm is a convex function

Pointwise maximum

if $f_1, \dots, f_m$ are convex, then $f(x) = \max\{f_1(x), \dots, f_m(x)\}$ is convex

• Proof

  Let $x, y\in \cap_{i = 1}^m \text{dom }f_i, \theta\ge 0$

  Since $f_i$ is a convex function,

  $$f_i(\theta x+(1-\theta)y)\le\theta f_i(x) + (1 - \theta)f_i(y)$$

  for all $i = 1,\dots, m$

  Without loss of generality, let $f(\theta x + (1 - \theta)y) = f_k(\theta x + (1-\theta)y)$

  Then,

  $$\begin{aligned}f(\theta x + (1 - \theta)y) &= f_k(\theta x + (1-\theta)y) \\ &\le \theta f_k(x) + (1-\theta)f_k(y) \\ &\le \theta f(x) + (1-\theta)f(y)\end{aligned}$$

  Therefore, $f$ is a convex function.

Examples

1. point-wise linear function

   $$f(x) = \max_{i = 1, \dots, m} a_i^Tx + b_i$$

   is a convex function

2. sum of $r$ largest components of $x\in \R^n$

   $$f(x) = x_{[1]} + \cdots + x_{[r]}$$

   where $x_{[i]}$ is i’th largest component of $x$

   is a convex function

   Actually,

   $$f(x) = \max\{x_{i_1} + x_{i_2} + \cdots + x_{i_r} |1\le i_1 < i_2 < \cdots i_r\le n\}$$

Pointwise supremum

if $f(x, y)$ is convex in $x$ for each $y\in \mathcal A$, then

$$g(x) = \sup_{y\in \mathcal A}f(x, y)$$

is convex

💡

$y$ can be abstracted object i.e. string

• Proof

  Let $x_1, x_2\in \text{dom }g, y\in \mathcal A, \theta\ge 0$

  $$g(\theta x_1+ (1 - \theta)x_2) = \sup_{y\in A}f(\theta x_1 + (1 - \theta)x_2, y)$$

  Since $f$ is convex in $x$ for each $y\in \mathcal A$,

  $$\begin{align}\sup_{y\in A}f(\theta x_1 + (1 - \theta) x_2, y) &\le \sup_{y\in \mathcal A}\bigg[\theta f(x_1, y) + (1-\theta)f(x_2, y)\bigg] \\ & \le \sup_{y\in \mathcal A}\theta f(x_1, y) + \sup_{y\in \mathcal A}(1-\theta)f(x_2, y) \\ &\le \theta g(x_1) + (1-\theta)g(x_2)\end{align}$$

  Therefore, $g$ is a convex set.

  Actually, we use the property of supremum

  $$\sup_x \bigg(f(x)+g(x)\bigg) \le \sup_x f(x) + \sup_x g(x)$$

  Let $\sup f(x) = \alpha, \sup g(x)= \beta$

  Since $\alpha\ge f(x_1)$ for all $x_1\in \text{dom }f$ and $\beta \ge f(x_2)$ for all $x_2\in \text{dom }g$, $\alpha + \beta \ge f(x) + g(x)$ for all $x \in \text{dom }f + g$

  So, $\alpha + \beta$ is a upper bound of $f + g$

  Therefore, $\sup_x \bigg(f(x)+g(x)\bigg) \le \sup_x f(x) + \sup_x g(x)$

Epigraph interpretation

In terms of epigraphs, the point-wise supremum of functions corresponds to the intersection of epigraphs: with $f, g$. we have

$$\text{epi }g = \bigcap_{y\in \mathcal A}\text{epi }f(\cdot, y)$$

Thus, the result follows from the fact that the intersection of a family of convex set is convex.

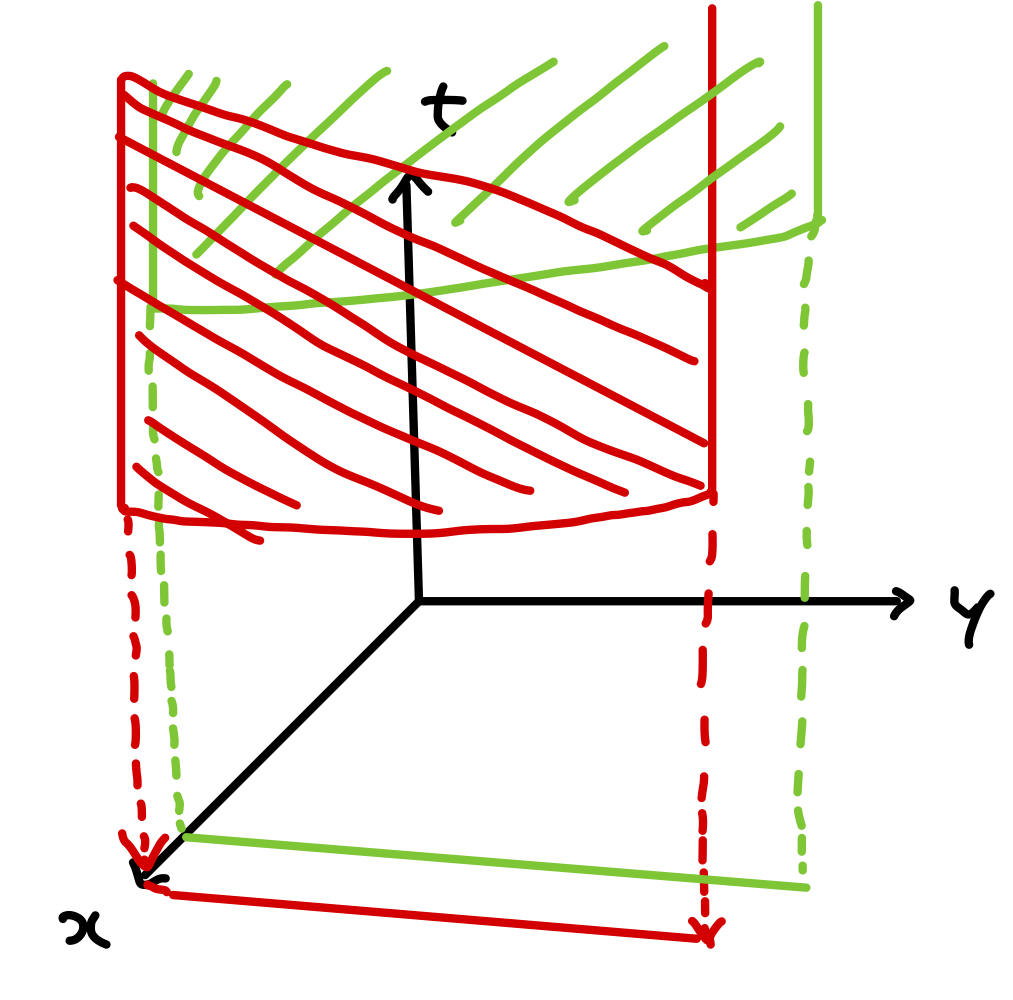
Red and green areas represent the epigraph of $f(x, y)$ for a fixed $x$. As $f$ is convex in $x$, both the red and green areas are convex sets. Our objective is to intersect the epigraph with a given point $x$ to determine the maximum (supremum) value for the given $x$.

Examples

1. support function of a set $C$

   $$S_C(x) = \sup_{y\in C}y^Tx$$

   

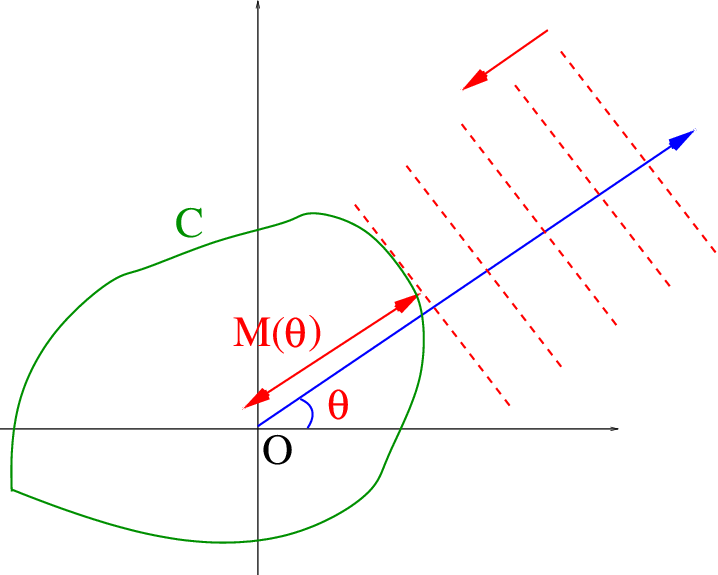
   The normal vector of the red dotted line is x

   💡

   Note that $C$ don’t have to be a convex set.

2. distance to farthest point in a set $C$

   $$f(x) = \sup_{y\in C}\|x - y\|$$

3. maximum eigenvalue of symmetric matrix

   $$\lambda_{\max}(X) = \sup_{\|y\|_2 = 1}y^TXy$$

   where $X\in S^n$

   💡

   $y^TXy$ is a linear function in $x$ for each $y$.

   • Proof

     Since $X \in S^n$, there exists an orthonormal basis by spectral theorem.

     Therefore,

     $$Xy = X\sum_{i = 1}^n y_ie_i = \sum_{i = 1}^ny_i\lambda_ie_i \\ \Rightarrow y^TXy = \sum_{i = 1}^n\lambda_i(y_i)^2$$

     First we want to show that $\max\{y_i|i = 1, \dots, n\}$ is a upper-bound of $y^TXy$

     Without loss of generality, $\max\{\lambda_i|i = 1, \dots, n\} = \lambda_k$

     $$\begin{aligned}\sum_{i = 1}^n \lambda_i(y_i)^2 &\le \lambda_k\bigg(\sum_{i = 1}^n(y_i)^2\bigg) \\ &\le \lambda_k\end{aligned}$$

     Given $\epsilon > 0$, we want to show that there exists $y_*$ such that

     $$\lambda_k -\epsilon < y_*^TXy_* < \lambda_k$$

     where $\|y_*\|_2 = 1$

     Without loss of generality, $\lambda_{l}$ is the second largest eigenvalue ($k \ne l)$

     Take $y_l = \sqrt{\frac{\epsilon}{2(\lambda_k - \lambda_l)}}, \;y_k = \sqrt{\frac{2(\lambda_k - \lambda_l) - \epsilon}{2(\lambda_k - \lambda_l)}}, \; y_j = 0$ if $j \ne k, l$

     Then,

     $$\sum_{i = 1}^n y_i = 1$$

     Moreover,

     $$\begin{aligned}\sum_{i = 1}^n \lambda_i(y_i)^2 &= \lambda_l \frac{\epsilon}{2(\lambda_k- \lambda_l)} + \lambda_k\frac{2(\lambda_k - \lambda_l) -\epsilon}{2(\lambda_k - \lambda_l)} \\ &= \frac{\lambda_l \epsilon + 2\lambda_k(\lambda_k - \lambda_l) -\lambda_k\epsilon}{2(\lambda_k - \lambda_l)} \\ &= \lambda_k - \frac{\epsilon}{2}\end{aligned}$$

     Therefore,

     $$\lambda_{\max}(X) = \sup_{\|y\|_2 = 1}y^TXy$$

Minimization

We have seen that the maximum and supremum of an arbitrary family of convex functions is convex. It turns out the some special forms of minimization also yields convex functions.

if $f(x, y)$ is convex in $(x, y)$ and $C$ is a convex set, then

$$g(x) = \inf_{y\in C}f(x, y)$$

where $g(x) > -\infty$ for all $x$

is convex.

We have to compare the condition for the point-wise supremum case. Note that $f(x,y)$ is convex in $(x, y)$. In point-wise supremum case, it is enough to satisfy only $x$

• Proof

  Let $x_1, x_2\in \text{dom g}, \theta \ge 0$

  For given $\epsilon > 0$, $\exists y_1, y_2\in C$ such that

  $$g(x_1) < f(x_1, y_1) < g(x_1) + \epsilon /2 \\ g(x_2) < f(x_2, y_2) < g(x_2) + \epsilon /2$$

  Therefore,

  $$\begin{aligned}g(\theta x_1 + (1- \theta)x_2) &= \inf_{y\in C } f(\theta x_1 + (1- \theta)x_2, y) \\ &\le f(\theta x_1 + (1-\theta)x_2, \theta y_1 + (1-\theta)y_2) \\ &\le f(\theta(x_1, y_1) + (1-\theta)(x_2, y_2)) \\ &\le \theta f(x_1, y_1) + (1-\theta) f(x_2, y_2) \\ &\le \theta g(x_1) + (1-\theta)g(x_2) + \epsilon\end{aligned}$$

  Since $\epsilon$ is arbitrary,

  $$g(\theta x_1 + (1-\theta)x_2) \le \theta g(x_1) + (1-\theta)g(x_2)$$

  Therefore, $g$ is a convex function.

  💡

  The fundamental idea is that we want to use convexity of $f$ that makes slightly bigger than we want. We can control the amount of its value by using the definition of infimum.

Epigraph interpretation

Assume the infimum over $y\in C$ is attained for each $x$ (i.e. $\{f(x, y) | y\in C\}$ is closed set for each $x$). We have

$$\text{epi }g = \{(x, t) |\; (x,y,t)\in \text{epi }f\text{ for some }y\in C\}$$

Since the projection of a convex set on some of its components is convex, $\text{epi }g$ is a convex set.

💡

Intuitively, we can interpret this as a projection of $\text{epi }f$ to $xt$ plane which is a convex set.

💡

Generally, the union of the convex set is not a convex set. So we can’t apply the same approach for the supremum or maximum case. Therefore, the condition for minimization case is stronger than them (i.e. convexity with respect to $(x, y)$)

Example

1. $f(x, y) = x^TAx + 2x^TBy + y^TCy$ with

   $$\begin{bmatrix}A & B \\ B^T &C\end{bmatrix} \succeq 0, \quad C\succ 0$$

   We can express $g(x) = \inf_y f(x, y)$ as

   $$g(x) = x^T(A-BC^{\dagger}B^T)x$$

   where $C^\dagger$ is the pseudo-inverse of $C$. Since $g$ is convex, $A-BC^{\dagger}B^T\succeq 0$

   If $C$ is invertible, then $A - BC^{-1}B^T$ is called the Schur complement of $C$ in the matrix

   $$\begin{bmatrix}A & B \\ B^T &C\end{bmatrix}$$

   💡

   A convex quadratic function and if minimize that function over some variables, the result is quadratic form.

   Shur's Complement

   유도방법 아래 링크의 1-2페이지 자료를 확인한다. 블록 행렬을 연립방정식 형태로 정리하고 해를 구함으로써 그 형태를 자연스럽게 이해할 수 있다. (link1) (link2)

   http://ranking.uos.ac.kr/blog_page/post_src/post20231031.html

2. distance to a set : $\text{dist}(x, S) =\inf_{y\in S}\|x-y\|$ is convex if $S$ is convex.

Composition with scalar functions

composition of $g:\R^n\to \R$ and $h : \R \to \R$

$$f(x) = h(g(x))$$

$f$ is convex if

1. $g$ convex, $h$ convex, $\tilde h$ non-decreasing

2. $g$ concave, $h$ convex, $\tilde h$ non-increasing

where $\tilde h$ is a extended value extension

💡

There are no assumption related to twice differentiability of $h$ and $g$

If we assume that $n = 1$ and twice differentiable for $g, h$ we can get an intuition

$$f''(x) = h''(g(x))g'(x)^2 + h'(g(x))g''(x)$$

Think about this example,

$$h(x) = x^2 \quad x\in \R_+$$

This function is trivially increasing. However,

$$\tilde h(x) = \begin{cases}x^2 \quad x\in \R_+ \\ \infty \quad \text{otherwise}\end{cases}$$

this function is not a increasing function.

Interpretation of $\tilde h$

To say that $\tilde h$ is nondecreasing means that for any $x, y\in \R$ ($x<y$), we have $\tilde h(x) \le \tilde h(y)$.

That means $y\in \text{dom h} \Rightarrow x\in \text{dom }h$

Therefore, the domain of $h$ extends infinitely in the negative direction; it is either $\R$ or an interval like $(-\infty, a)$ or $(\infty, a]$

Similarly, $\tilde h$ is non-increasing means that the domain of $h$ extends infinitely in the positive direction; it is either $\R$ or an interval like $(a, \infty)$ or $[a, \infty)$

• Proof

  Let $g$ is convex, $h$ is convex, $\tilde h$ is nondecreasing and $x,y\in \text{dom }f, \theta \ge 0$.

  Since $x, y\in \text{dom }f$, $x, y\in \text{dom }g$

  Moreover we already know that $g$ is convex,

  $$g(\theta x + (1-\theta)y)\le \theta g(x) + (1-\theta)g(y)$$

  Similarly since $x,y\in \text{dom }f$,

  $$g(x), g(y)\in \text{dom h} \\ \Rightarrow \theta g(x) + (1-\theta)g(y)\in \text{dom }h \text{ (since dom h is convex set)} \\ \Rightarrow g(\theta x + (1-\theta)y)\in \text{dom }h \text{ (since }\tilde h \text{ is non-decreasing)}$$

  Since $\tilde h$ is non-decreasing,

  $$h(g(\theta x + (1-\theta)y)) \le h(\theta g(x) + (1-\theta)g(y))$$

  In addition, since $\theta g(x) + (1-\theta) g(y)\in \text{dom }h$ and $h$ is a convex function,

  $$h(\theta g(x) + (1-\theta)g(y)) \le \theta h(g(x))+ (1-\theta)h(g(y))$$

  Therefore,

  $$h(g(\theta x + (1-\theta)y)) \le \theta h(g(x)) + (1-\theta)h(g(y))$$

  Therefore $h\circ g$ is a convex function.

Examples

1. $\exp g(x)$ is convex if $g$ is convex

   💡

   We already know that exponential function is convex and increasing function on $\R$

2. $1/g(x)$ is convex if $g$ is concave and positive.

   💡

   We already know that $1/x$ is concave and non-increasing

Vector composition

composition of $g:\R^n\to \R^k$ and $h: \R^k \to \R$

$$f(x) = h(g(x)) = h(g_1(x), g_2(x), \dots, g_k(x))$$

$f$ is convex if

1. $g_i$ affine, $h$ convex

2. $g_i$ convex, $h$ convex, $\tilde h$ non-decreasing in each argument

3. $g_i$ concave, $h$ convex, $\tilde h$ non-increasing in each argument

where $\tilde h$ is a extended value extension

• Proof

  Without loss of generality, assume that $g_i$ convex, $h$ convex, $\tilde h$ non-decreasing in each argument.

  Let $x,y\in \text{dom f}, \theta\ge 0$ (i.e. $x, y\in \text{dom }g_i$ for each $i$ and $g(x),g(y)\in \text{dom }h$)

  Since $g_i$ is a convex function and $x, y\in \text{dom }g_i$

  $$g_i(\theta x + (1- \theta)y) \le \theta g_i(x) + (1-\theta) g_i(y)$$

  Since $h$ is convex, $\pi_i(\text{dom }h)$ is a convex set for each $i$.

  So,

  $$\theta g_i(x) + (1-\theta)g_i(y) \in \pi_i(\text{dom }h), \forall i$$

  Therefore,

  $$\theta g(x) + (1-\theta)g(y)\in \text{dom h}$$

  Moreover, $\tilde h$ is non-decreasing in each argument and $\theta g_i(x) + (1- \theta)g_i(y)\in \pi_i(\text{dom }h),\forall i$,

  $$g_i(\theta x+(1 - \theta)y) \in \pi_i(\text{dom }h), \forall i$$

  Therefore,

  $$g(\theta x + (1-\theta)y) \in \text{dom }h$$

  In addition,

  $$\begin{aligned}h(g(\theta x + (1-\theta)y)) &= h(g_1(\theta x + (1-\theta)y), \cdots , g_k(\theta x + (1-\theta)y)) \\ &\le h(\theta g_1(x) + (1-\theta)g_1(y), \cdots, g_k(\theta x + (1-\theta)y)) \\ &\le h(\theta g_1(x) + (1-\theta)g_1(y), \cdots, \theta g_k(x) + (1- \theta)g_k(y)) \\ &= h(\theta(g_1(x), \cdots, g_k(x)) + (1-\theta)(g_1(y), \cdots, g_k(x))) \\ &= h(\theta g(x) + (1-\theta)g(y)) \\ & \le \theta h(g(x)) + (1-\theta)h(g(y)) \text{ (since }h \text{ is convex)}\end{aligned}$$

  Therefore $h\circ g$ is a convex function.

  If $g_i$ is a affine function,

  $$g_i(\theta x + (1-\theta)y)= \theta g_i(x) + (1-\theta) g_i(y) \\ g_i(\theta x+ (1-\theta)y)) \in \pi_i(\text{dom }h)$$

  Therefore, there is no requirement of non-increasing or non-decreasing condition of $h$ in this case.

We can actually interpret some convex preserving operations by using vector composition.

1. adding convex function

   We can interpret $h$ as a summation of each argument. We already know that that kind of function is convex. (Actually, it is affine)

   Moreover $\tilde h$ nondecreasing in each argument.

   Therefore, it is a convex function

2. maximum values within convex functions

   We can interpret $h$ as a maximum of each argument. We already know that max function is convex. Moreover $\tilde h$ is non-decreasing in each argument.

   Therefore, it is a convex function.

Examples

1. $\sum_{i = 1}^m \log g_i(x)$ is concave if $g_i$ are concave and positive

   💡

   Since we already know that log function is concave and it is non-decreasing

2. $\log\sum_{i = 1}^m \exp g_i(x)$ is convex if $g_i$ are convex.

   💡

   Since we already know that $\log\sum_{i = 1}^m \exp z_i$ is a convex function and it is non-decreasing for each argument.

Perspective

the perspective of a function $f:\R^n\to \R$ is the function $g:\R^n\times \R \to \R$

$$g(x, t) = tf(x/t), \quad \text{dom } g = \{(x, t)|x/t\in \text{dom }f, t> 0\}$$

if $f$ is convex, then $g$ is convex.

• Proof

  $$\begin{aligned}(x, t, s)\in \text{epi }g &\Leftrightarrow tf(x/t)\le s \\ &\Leftrightarrow f(x/t) \le s/t \\ &\Leftrightarrow (x/t, s/t)\in \text{epi }f\end{aligned}$$

  Since $f$ is a convex function, $\text{epi }f$ is a convex sets. Moreover, perspective function preserve a convexity. So, $\text{epi }g$ is a convex set.

  Therefore, $g$ is a convex function.

Example

1. $f(x) = x^Tx$ is convex, $g(x, t) = x^Tx/t$ is convex for $t>0$

2. negative logarithm : $f(x) = -\log x$ is convex; hence relative entropy (a.k.a KL divergence)

   $$\begin{aligned}g(x, t) &= t\log t - t\log x \\ &= -t\log\frac{x}{t}\end{aligned}$$

   is convex on $\R_{++}^2$

3. if $f$ is convex, then

   $$g(x) = (c^Tx+d)f((Ax+b)/(c^Tx + d))$$

   is convex on $\{x|\; c^Tx+d > 0, (Ax+b)/(c^Tx+d)\in \text{dom }f\}$

   💡

   We already know that $f(Ax + b)$ is convex

Conjugate function

the conjugate of a function $f$ is

$$f^*(y) = \sup_{x\in \text{dom }f}(y^Tx - f(x))$$

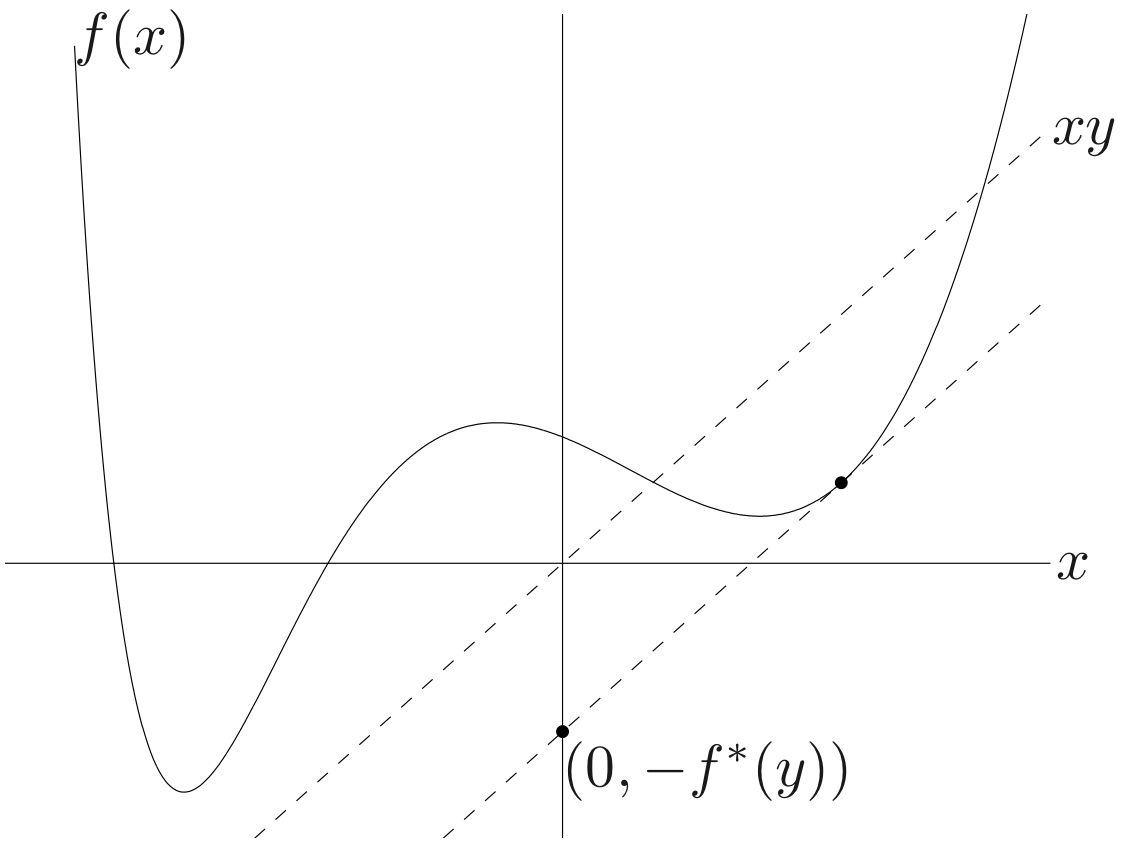
Let $f(x)$ is a making cost, $x$ is the number of product, $y$ is the price for each product.

We want to maximize the profit. So our goal is to find the number of product maximize our benefit.

Note that $f^*$ is convex (even if $f$ is not)

• Proof

  $y^Tx - f(x)$ is affine with respect to $y$.

  Moreover, it is the point-wise supremum of a family of convex (indeed, affine) functions of $y$. Therefore, it is actually a corollary of the supremum of the convex function is a convex function.

💡

The conjugate function, also known as the Legendre-Fenchel transform, is a powerful tool in convex analysis that allows us to recover info rmation about a given function. It provides a way to characterize the dual properties of a function, revealing its convexity, smoothness, and other important properties.

Examples

1. negative logarithm : $f(x) = -\log x$

   $$\begin{aligned}f^*(x) &= \sup_{x>0}(xy + \log x) \\ &= \begin{cases}-1-\log(-y) & y< 0 \\ \infty &\text{otherwise}\end{cases}\end{aligned}$$

2. strictly convex quadratic : $f(x) = (1/2)x^TQx$ with $Q\in S_{++^n}$

   $$\begin{aligned}f^*(y) &= \sup_x (y^Tx - (1/2)x^TQx) \\ &= \frac{1}{2}y^TQ^{-1}y\end{aligned}$$

   💡

   Conjugate of quadratic form is the inverse matrix

Quasi-convex functions

$f:\R^n\to \R$ is quasi-convex if $\text{dom }f$ is convex and the sublevel sets

$$S_\alpha = \{x\in \text{dom }f|\; f(x) \le \alpha\}$$

are convex for all $\alpha$

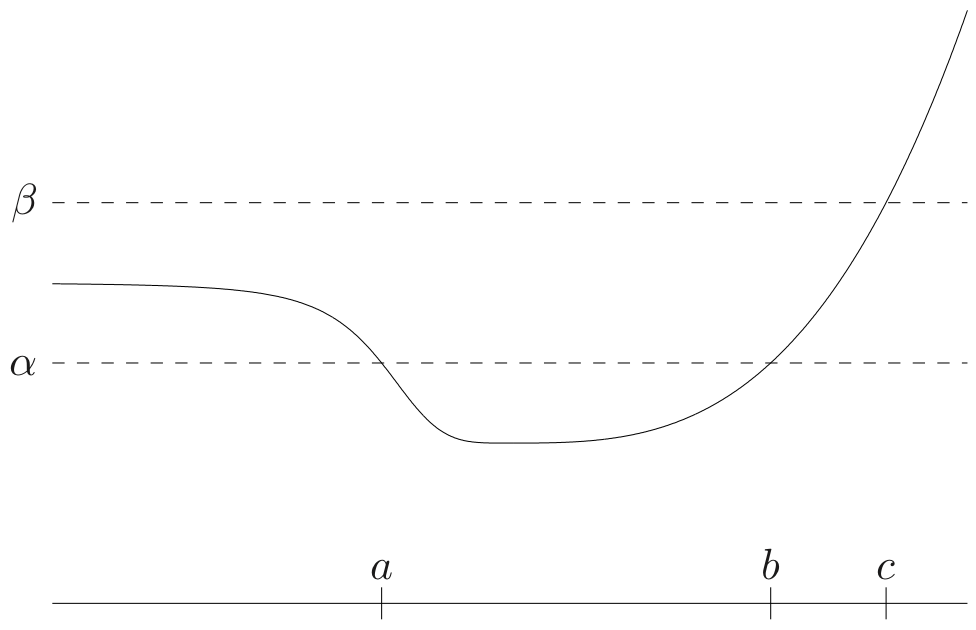
A function is quasi-concave if $-f$ is quasi-convex. A function that is both quasi-convex and quasi-concave is called quasi-linear.

Convex functions have convex sub-level sets, and so are quasi-convex.

• Proof

  We already know that epigraph of a convex function is a convex set. Moreover, $\{(x, y) | \; y \le \alpha\}$ is a convex set.

  Since the intersection of convex sets is also a convex set.

  Therefore,

  $$\{(x, f(x)) |\; f(x) \le \alpha, x\in \text{dom }f\}$$

  is a convex set.

  Moreover, we already know that projection of certain coordinate is also a convex set. Therefore,

  $$\{x \in \text{dom }f|\; f(x) \le \alpha\}$$

  is a convex set.

  Therefore, every convex function is a quasi-convex function.

Examples

1. $\sqrt {|x|}$ is quasi-convex on $\R$

   

2. $\text{ceil}(x) = \inf \{z\in \Z|\; z\ge x\}$ is quasi-linear

   

3. $\log x$ is quasi-linear on $\R_{++}$

4. $f(x_1, x_2) = x_1x_2$ is quasi-concave on $R_{++}^2$

5. linear-fractional function

   $$f(x) = \frac{a^Tx + b}{c^Tx + d} \quad \text{dom} f = \{x | \; c^Tx + d > 0\}$$

   is quasi-linear

   💡

   Note that the sublevel set is half space

6. distance ratio

   $$f(x) = \frac{\|x-a\|_2}{\|x-b\|_2} \quad \text{dom }f = \{x |\; \|x-a\|_2\le \|x-b\|_2\}$$

   is quasi-convex.

   • Proof

     We want to know whether $\{x\in \text{dom }f |\; f(x) \le t\}$ is a convex set or not for all $a$. (For simplicity, we assume that $t$ is non-negative.)

     Take $g : \R^2 \to \R$, $h_1 : \R\to \R, h_2 : \R \to \R$ as follows

     $$h_1(x) = \|x-a\|_2 \\ h_2(x) = \|x-b\|_2 \\ g(x_1, x_2) = x_1 - tx_2 \quad$$

     Since $h_1, h_2$ are convex and $\tilde g$ are non-decreasing and non-increasing respectively (if $t$ is negative, $\tilde g$ are both non-decreasing), $g(h_1(x), h_2(x))$ is a convex function.

     As we proved above, every convex function is also a quasi-convex funciton.

     Therefore,

     $$\{x |\; \|x-a\|_2 - t\|x-b\|_2 \le 0\} \Leftrightarrow \{x|\; \frac{\|x - a\|_2}{\|x - b\|_2} \le t\}$$

     is a convex set.

     Since $t$ is arbitrary,

     $$\{x |\; \|x-a\|_2 - 1\|x-b\|_2 \le 0\} \Leftrightarrow \{x|\; \|x-a\|_2 \le \|x-b\|_2\}$$

     is a convex set.

     Therefore,

     $$\{x|\frac{\|x - a\|}{\|x-b\|}\le t \text{ and }\|x-a\|_2 \le \|x-b\|_2\}\\ \\\Leftrightarrow \{x\in \text{dom }f |\; f(x) \le t\}$$

     Therefore, $f$ is a quasi-convex function.

Properties

1. modified Jensen’s inequality : for quasi-convex $f$

   $$0\le \theta \le 1 \Rightarrow f(\theta x + (1-\theta)y) \le \max \{f(x), f(y)\}$$

   

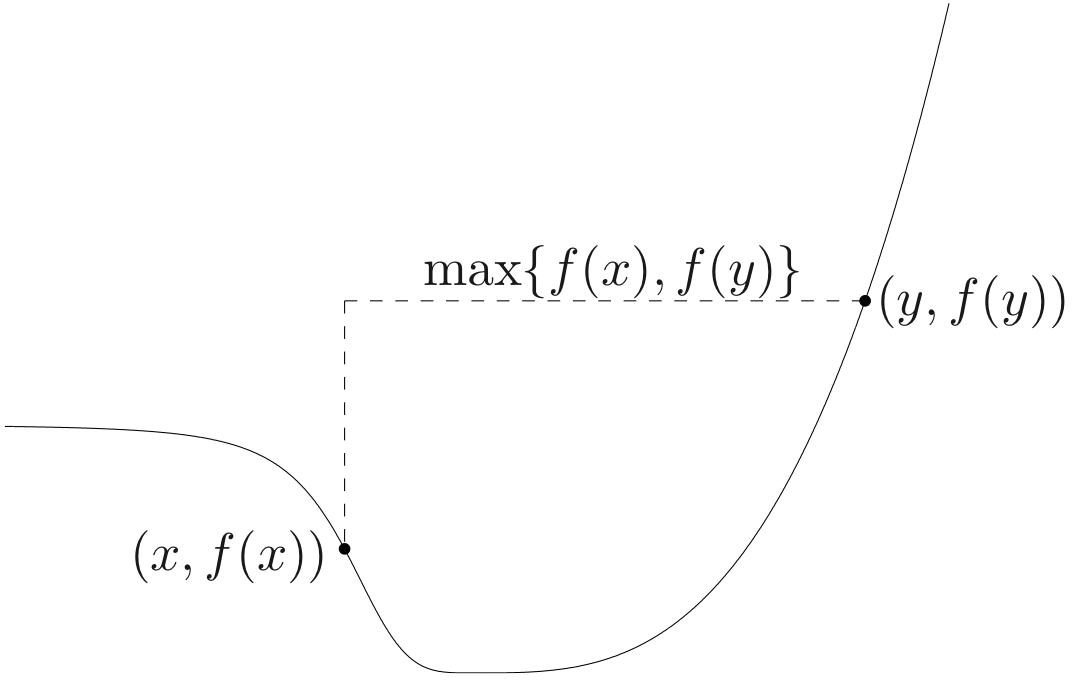
   • Proof

     Since $f$ is a quasi-convex function,

     $$\{t\in \text{dom }f | \; f(t) \le f(x)\} \\ \{t\in \text{dom }f | \; f(t) \le f(y)\}$$

     are a convex set.

     We already know that intersection of two convex sets is also a convex set. Therefore,

     $$\{t\in \text{dom f} |\; f(t) \le \max\{f(x), f(y)\}$$

     is a convex set.

     For simplicity, let’s say

     $$A =\{t\in \text{dom f} |\; f(t) \le \max\{f(x), f(y)\}$$

     Trivially, $x, y\in A$. Therefore, for given $\theta \ge 0$,

     $$\theta x + (1-\theta)y \in A$$

     So,

     $$f(\theta x + ( 1 - \theta)y) \le \max \{f(x), f(y)\}$$

2. first-order condition : Suppose $f :\R^n \to \R$ is differentiable with $\text{dom }f$ is convex. Then $f$ is quasi-convex if and only if

   $$\forall x, y\in \text{dom }f, f(y)\le f(x) \Rightarrow \nabla f(x)^T (y- x)\le 0$$

   

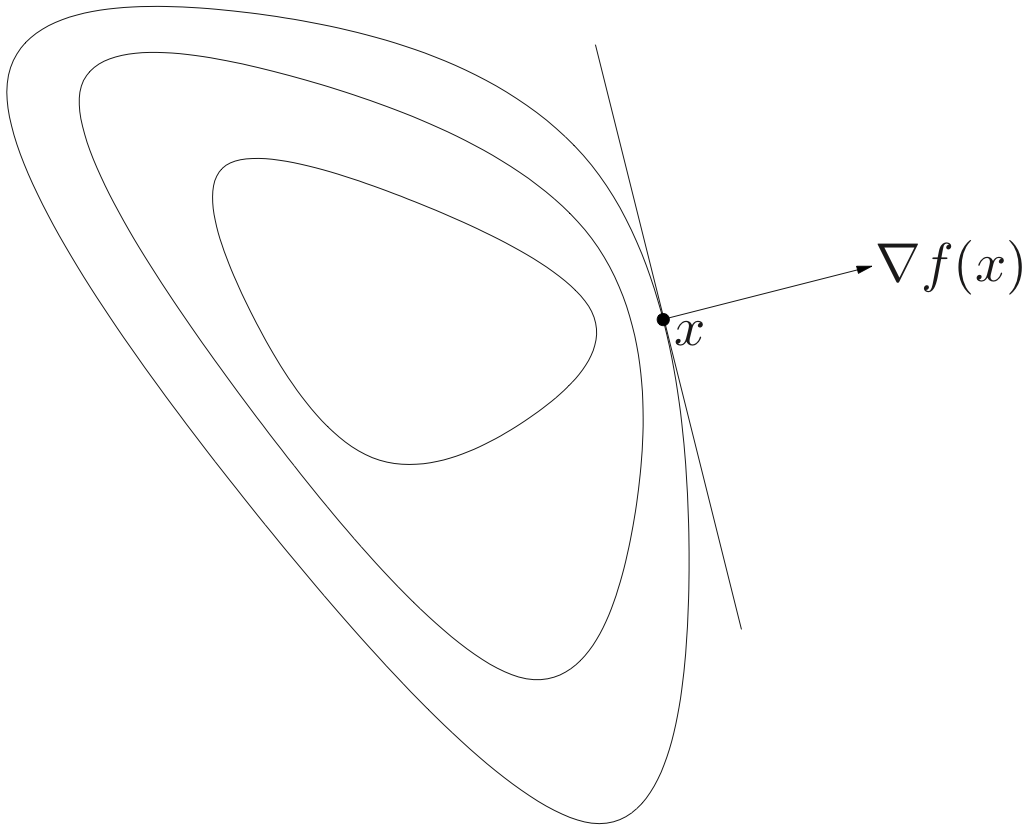
   • Proof

     Let $f$ is quasi-convex. Then

     $$A = \{y\in \text{dom }f|\; f(y) \le f(x)\}$$

     is a convex set.

     Suppose $\exists y\in A$ such that

     $$\nabla f(x)^T(y - x) > 0$$

     Then, $\exists 0< \epsilon < 1$ such that

     $$f(x+ (y - x)\epsilon) > f(x)$$

     Since $x, y\in A$ and $A$ is a convex set,

     $$x + (y - x) \epsilon \in A$$

     It is contradicts to the definition of $A$.

     Therefore,

     $$\forall x, y\in \text{dom }f, f(y)\le f(x) \Rightarrow \nabla f(x)^T (y- x)\le 0$$

     We want to show that for given $a$

     $$\{x \in \text{dom }f |\; f(x) \le a\}$$

     is a convex set

     1. case 1 : $\exist x\in \text{dom }f$ such that $f(x) = a$

        By assumption,

        $$y \in \{x \in \text{dom }f |\; f(x) \le a\} \Rightarrow \nabla^2f(x)^T (y - x)\le 0 \\ \Rightarrow y\in \text{dom f}\cap \{y | \nabla^2f(x)^T(y- x)\le 0\}$$

        Since $\nabla^2 f(x)^T(y -x)$ is affine with respect to $y$, $\{y | \nabla^2f(x)^T(y- x)\le 0\}$ is a convex set.

        Therefore $\{x\in \text{dom }f |f(x)\le a\}$ is a convex set.

     2. case 2 : $\nexists x\in \text{dom }f$ such that $f(x) = a$

        Since $f$ is differentiable, $f$ is continuous for every $x$. Therefore, there are only two cases.

        1. $f(x) > a, \forall x$

           In this case, there is no element in sub-level set. Therefore, it is a vacuously true to satisfy the convexity.

        2. $f(x) < a, \forall x$

           In this case, $\{x\in \text{dom }f| f(x) \le a\} = \text{dom }f$. We already know that $\text{dom }f$ is a convex set.

        Therefore $\{x\in \text{dom }f |f(x)\le a\}$ is a convex set.

   💡

   Taking into account that the sublevel set of a quasi-convex function is a convex set, one can understand the above concept as a restriction of the comparison region.

💡

Note that sums of quasi-convex functions are not necessarily quasi-convex.

Log-concave and log-convex functions

a positive function $f$ is log-concave if $\log f$

$$f(\theta x + (1-\theta)y)\ge f(x)^\theta f(y)^{1-\theta}$$

for $0\le \theta \le 1$

$f$ is log-convex if $\log f$ is convex.

Examples

1. powers : $x^a$ on $\R_{++}$ is log-convex for $\alpha \le 0$, log-concave for $\alpha \ge 0$
   • proof

     $$a\log(\theta x + (1-\theta)y) \ge a\theta\log(x) + a(1-\theta)\log(y)$$

     if $a \ge 0$,

     $$\log(\theta x + (1-\theta)y) \ge \theta\log(x) + (1-\theta)\log(y)$$

     the above function is log-concave.

     if $\alpha \le 0$,

     $$\log(\theta x + (1-\theta)y) \le \theta\log(x) + (1-\theta)\log(y)$$

     the above function is log-convex.

2. many common probability densities are log-concave (ex : normal dist)

   $$f(x) = \frac{1}{\sqrt{(2\pi)^n\det\Sigma}}e^{-\frac{1}{2}(x-\bar x)^T\Sigma^{-1}(x-\bar x)}$$

   💡

   If we take logarithm for above function, it is just a quadratic function.

3. cumulative Gaussian distribution $\Phi$ is log-concave.

   $$\Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^x e^{-u^2/2}du$$

Properties

1. twice differentiable $f$ with convex domain is log-concave if and only if

   $$f(x)\nabla^2f(x) \preceq \nabla f(x) \nabla f(x)^T$$

   for all $x\in \text{dom }f$

   or equivalently

   $$\nabla^2 f(x) \preceq \frac{\nabla f(x) \nabla f(x)^T}{f(x)}$$

   for all $x\in \text{dom }f$

   The condition for concave function is 0 for the right side of the above inequality. In log-concave case, the hessian matrix is less than equal to the rank-one matrix. That means we can have at most one positive eigenvalue of the hessian.

   💡

   For a rank-one matrix $A = uv^T$, there is exactly one non-zero eigenvalue, and it is equal to the dot product $u^Tv$

2. product of log-concave functions is log-concave

   💡

   basically related to the sum of the concave function is concave.

3. sum of log-concave functions is not always log-concave

   💡

   mixture of log-concave distribution is not always log-concave

4. integration : if $f:\R^n\times \R^m \to \R$ is log-concave, then

   $$g(x) = \int f(x,y)dy$$

   is log-concave.

   Prékopa–Leindler inequality

   In mathematics, the Prékopa–Leindler inequality is an integral inequality closely related to the reverse Young's inequality, the Brunn–Minkowski inequality and a number of other important and classical inequalities in analysis. The result is named after the Hungarian mathematicians András Prékopa and László Leindler.&#91;1&#93;&#91;2&#93;

   https://en.wikipedia.org/wiki/Prékopa–Leindler_inequality

Consequences of integration property

1. convolution $f* g$ of log-concave functions $f, g$ is log-concave

   $$(f*g)(x) = \int f(x-y)g(y)dy$$

2. if $C\sub \R^n$ convex and $y$ is a random variable with log-concave pdf then

   $$f(x) = \text{Prob}(x + y\in C)$$

   is log-concave

   • Proof

     Write $f(x)$ as integral of product of log-concave functions

     $$f(x) =\int g(x+ y)p(y)dy$$

     where

     $$g(u) = \begin{cases}1 & u\in C \\ 0 & u\notin C\end{cases}$$

     $p$ is pdf of $y$

Convexity with respect to generalized inequalities

Suppose $K\sub \R^m$ is a proper cone with associated generalized inequality $\preceq_K$. We say $f:\R^n\to \R^m$ is $K$-convex if for all $x, y$, and $0\le \theta \le 1$,

$$f(\theta x + (1-\theta)y)\preceq_K\theta f(x) + (1-\theta) f(y)$$

The function is strictly $K$-convex if

$$f(\theta x + (1-\theta)y)\prec_K\theta f(x) + (1-\theta) f(y)$$

for all $x\ne y$ and $0 < \theta <1$

💡

These definitions reduce to ordinary convexity and strict convexity when $m = 1$ and $K = \R^{++}$