2. Optimality Conditions, Convexity, Newton’s Method for Equations

Optimality Conditions: Preliminaries

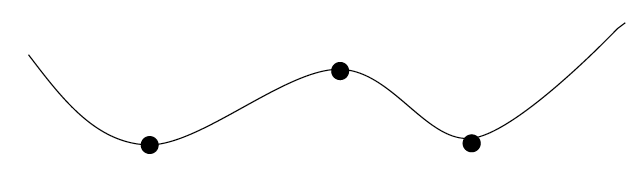
• Local minima and maxima have one thing in common

  $$\nabla f(x) = 0$$

First-order Necessary Condition

From now on $f$ is differentiable and that its first and second derivatives are continuous for every $x\in X$ where $X$ is a domain of $f$

If $x^*$ is a local minimum, then

$$\nabla f(x^*) = 0$$

• Not a sufficient condition, since it could be a saddle point

  

Second-order Conditions

If $x^*$ is a local minimum, then $\nabla^2 f(x^*)$ is positive semi-definite

• Proof

But you should note that even though $\nabla f(x^*) = 0$ and $\nabla^2f(x^*) \ge 0$, we can’t be sure that $x^*$ must be a local minimum.

Think about,

$$f(x_1, x_2) =x_1^3 + x_2^3$$

That means there is no sufficient and necessary condition in general

💡

First-order Condition과 Second-order Condition은 local minimum이면 만족하지만 그것을 만족한다고 해서 local minimum이라고 확신할 수 없다는 것이다.

Second-order sufficient condition

It is sufficient to guarantee that $x^*$ is a local minimizer. If

$$\nabla f(x^*) = 0 \text{ and } \nabla^2 f(x^*) \text{ is positive definite}$$

then $x^*$ is a strict local minimizer of $f$.

• Proof

  Since $\nabla f(x^*) = 0,$

  $$f(x^* + p) = f(x^*) + \frac{1}{2}v^T\nabla^2f(\zeta)v$$

  where $\zeta \in N_p(x^*)$

  Since $\nabla^2f$ is continuous, $\exists \delta$ such that

  $$\|\zeta - x^*\| < \delta \Rightarrow \|\nabla^2f(\zeta) - \nabla^2f(x^*)\| < \frac{1}{2}v^T\nabla^2f(x^*)v$$

  Take $v = \min(1, \delta)$

  💡

  Note that $\zeta \in N_v(x^*)$

  Moreover, since $\nabla^2 f(x^*)$ is positive definite,

  $$v^T\nabla^2f(x^*)v > 0, \forall \text v{ (}v\ne 0)$$

  $$\begin{align}v^T\nabla^2f(x^*)v - v^T\nabla^2f(\zeta)v &= v^T(\nabla^2f(x^*) - \nabla^2f(\zeta) )v \\ & \le \|v\|\|(\nabla^2f(x^*) - \nabla^2f(\zeta) )v\| \\ & \le \|v\|\|\nabla^2f(x^*) - \nabla^2f(\zeta)\|\|v\| \\ & \le \|v\|^2\|\nabla^2f(x^*) - \nabla^2f(\zeta)\| \\ & \le \frac{1}{2}v^T\nabla^2f(x^*)v\end{align}$$

  💡

  1) bi-linearity of inner-product

  2) Cauchy-schwarz inequality

  3) defi

  4) Associativity of multiplication in $\R$

  Therefore,

  $$0 < \frac{1}{2}v^T\nabla f(x^*)v \le v^T\nabla^2f(\zeta)v$$

  This means that $\nabla^2f(\zeta)$ is also positive definite. So, $x^*$ is a local minimum.

  💡

  Since $v$ has a restriction on its domain, we can not guarantee that $x^*$ is a global minimum.

Convexity

• A set $S$ is convex if any $x\in S$ and $y \in S$,

$$\alpha x + (1-\alpha)y \in S, \forall \alpha \in[0, 1]$$

• A function $f$ is convex on a convex set $S$ if for any $x\in S$ and $y \in S$,

  $$f(\alpha x+ (1-\alpha)y) \le \alpha f(x) + (1-\alpha)f(y), \forall \alpha\in [0, 1]$$

• A minimization problem is convex if $f$ is convex and $S$ is convex

Implication of Convexity

For a convex optimization problem, a local optimum $x^*$ is also a global optimum

If the feasible region is convex, it implies that all the points along the line segment between the current solution and the new feasible solution are also feasible.

Therefore, any smaller step size will still allow us to move along the same direction from the current solution, while remaining within the feasible region. This is because the convexity property guarantees that the entire line segment between the current solution and the new feasible solution lies within the feasible region.

This property is valuable in optimization algorithms, as it ensures that if we have found a feasible solution, we can always refine it further by taking smaller steps while maintaining feasibility. It provides flexibility in adjusting the step size and allows for a more precise exploration of the feasible region.

How to recognize convexity?

1. One dimension case : A function $f$ is convex if and only if $f''(x) \ge 0$ for all $x\in X$ where $X$ is a domain of $f$

2. Multiple dimension case
   • $f$ is convex if and only if Hessian $\nabla^2 f(x) \ge 0$ for all $x \in X$ where $X$ is a domain of $f$
   • If $\nabla^2 f(x)$ is positive definite for all $x\in X$ (i.e. $\nabla^2 f(x) > 0, \forall x \in X)$, then $f$ is strictly convex

     → Note that it is not true for opposite direction

   • $f$ is convex if and only if it is above the tangent

     

     $$f(y) \ge f(x) + \nabla f(x)(y - x), \forall x, y\in X$$

💡

With constraints, we care more about function’s convexity over the feasible set; the above remains applicable but may require minor rephrasing

Convexity and Optimality Condition

Actually if $f$ is convex, local optimum and global optimum is equivalent. In addition,

$$\nabla f(x^*) = 0 \Leftrightarrow x^*\text{ is global minimum}$$

💡

Second-order Condition is already satisfy if $f$ is convex

Newton’s Method for Nonlinear Equations

• A sequence of points as approximate solutions

• The sequence converges if it approaches a solution of the equation

  Especially for one dimension,

  $$f(x_k + p) \approx f(x_k) + pf'(x_k)$$

  This means that

  $$f(x_k) + pf'(x_k) = 0 \rightarrow p = -\frac{f(x_k)}{f'(x_k)}$$

  Therefore,

  $$x_{k + 1} = x_k - \frac{f(x_k)}{f'(x_k)}$$

  • This is the Newton-Raphson method

  

  Newton's method

  In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. The most basic version starts with a real-valued function f, its derivative f′, and an initial guess x0 for a root of f. If f satisfies certain assumptions and the initial guess is close, then

  https://en.wikipedia.org/wiki/Newton's_method

• A related derivative-free method is the secant method

  

  $$x_{k + 1} = x_k - f(x_k)\frac{x_k - x_{k - 1}}{f(x_k) - f(x_{k - 1})}$$

  💡

  It can be viewed as approximate of the derivative by using average rate of change.

  Secant method

  In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite-difference approximation of Newton's method. However, the secant method predates Newton's method by over 3000 years.

  https://en.wikipedia.org/wiki/Secant_method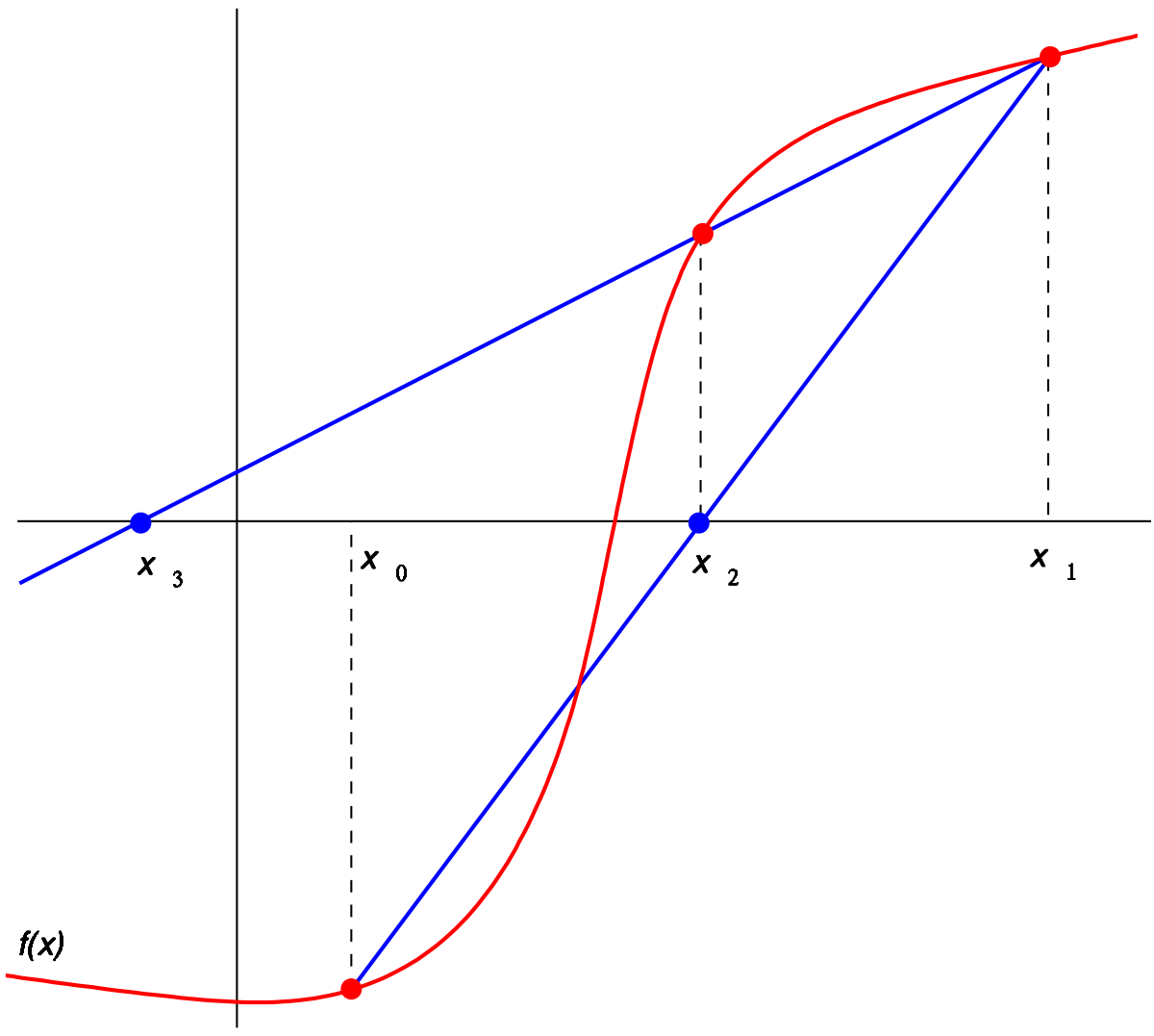

  

• Convergent or not: depends on the function and the initial point

Newton’s Method: Multiple Dimensions

Let $g : \R^n \to \R^n$

$$g(x_k+ p) = g(x_k) + \nabla g(x_k)p$$

That means

$$g(x_k) + \nabla g(x_k)p = 0 \Leftrightarrow p = -\nabla g(x_k)^{-1}g(x_k)$$

if $\nabla g(x_k)$ is invertible

Therefore,

$$x_{k + 1} = x_k - \nabla g(x_k)^{-1}g(x_k)$$

💡

If $\nabla g(x_k)$ is not invertible, this method can’t be applicable.

💡

If we interpret $\nabla g(x_k)^{-1}$ as a $\frac{1}{g'}$, it is just a generalization of the newton’s method in 1-dimensional case.