1. Basics

A Generic Optimization Model

$$\min f(x_1, x_2, \dots, x_n)$$

$\text{subject to}$

$$\begin{align}g_1(x_1, x_2, \dots, x_n) \le b_1 \\ g_2(x_1, x_2, \dots, x_n) \le b_2 \\ \vdots \\ g_m(x_1, x_2, \dots, x_n) \le b_m \end{align}$$

In compact form

$$\min f(x)$$

where $x\in S$ ($S$ : the set of all feasible solutions permitted by the constraints)

Assumptions

• Continuous variables, smooth functions (twice continuously differentiable unless stated otherwise)

• Linear programming (LP) and Non-linear programming (NLP)

• What do we mean by solving the problem?
  • LP : compute the optimum
  • NLP : hard in general; we focus on a local optimum

Boundary and Interior

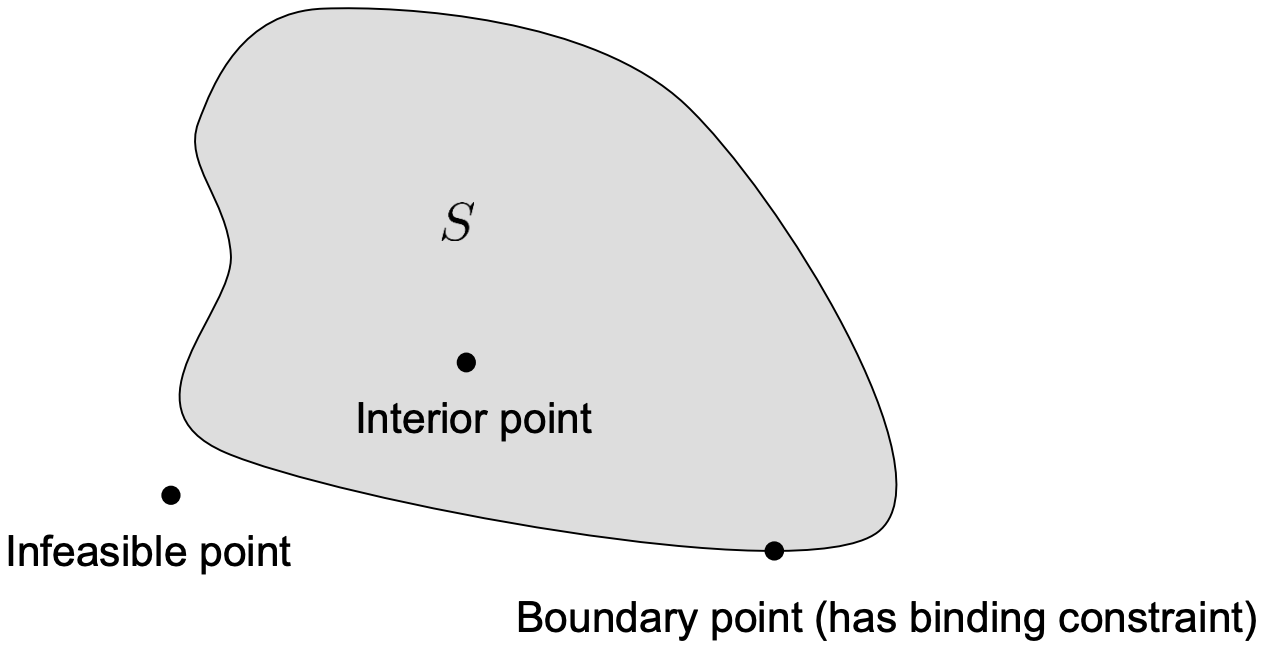
• Boundary of $S$ : formed by all feasible points with at least one binding constraint; binding = an inequality is satisfied as equality

• Interior of $S$ : the rest of $S$, or all feasible points without any binding constraint

Global and Local Optima

• $x^*$ is a global minimum if $f(x^*) \le f(x), \forall x\in S$

• $x^*$ is a local minimum if $f(x^*) \le f(x), \forall x\in S$ such that $d(x^*, x) \le \epsilon$

In general, it is difficult to find the global minimum.

Therefore, we will focus on finding a local minimum in nonlinear optimization problems.

How to Solve it?

• Take a sequence of steps to improve the objective function

• Convergence : A point that is locally optimal

General Algorithm

1. Specify some initial guess of the solution $x_0$

2. For k = 0, 1, …
   1. If $x_k$ is locally optimal, stop
   2. Determine a search direction $p_k$
   3. Determine a step length $\alpha_k$, such that $x_{k + 1} = x_k + \alpha_kp_k$ is a better solution than $x_k$

💡

Technically, we have to consider about the shape at the point.

Descent Direction

• It is desirable to have descent direction as our search direction

• Formal definition

  A direction $p$ of function $f$at point $x$ is a descent direction, if there exists $\epsilon$ such that $f(x+\alpha p) < f(x), 0 < \alpha \le \epsilon$

Note

Any direction $p$ less than $90^\circ$ from $-\nabla f(x)$ is a descent direction

Hessian

Second-order derivative of a function $f$ in several variables is called the Hessian

$$\nabla^2f = \begin{bmatrix}\frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1\partial x_2} &\cdots & \frac{\partial^2f}{\partial x_1 \partial x_n}\\ \frac{\partial^2f}{\partial x_2\partial x_1} & \frac{\partial^2f}{\partial x_2^2} &\cdots & \frac{\partial^2f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \vdots & \vdots \\\frac{\partial^2f}{\partial x_n\partial x_1} & \frac{\partial^2f}{\partial x_n\partial x_2} &\cdots & \frac{\partial^2f}{\partial x_n^2}\end{bmatrix}$$

The Hessian is a square and symmetric matrix

It is useful for optimality check, and function approximation.

Taylor Series

1. One dimension

   $$f(x_0 + p) \approx f(x_0) + pf'(x_0) + \frac{1}{2}p^2f''(x_0) + \cdots$$

2. Multiple dimensions

   $$f(x_0 + p) \approx f(x_0) + p^Tf'(x_0) + \frac{1}{2}p^Tf''(x_0)p + \cdots$$

What about approximating $f$ at point $x_0$ with $f(x_0) + p^T\nabla f(x_0)$ and find the best possible $p$ for the approximation?

$$\min_p f(x_0) + p^T\nabla f(x_0)$$

What about adding one more term in the approximation?

$$\min_p f(x_0) + p^T\nabla f(x_0) + \frac{1}{2}p^T\nabla^2f(x_0)p$$

Sensitivity (Conditioning)

• There may be errors in the input data

• Also, data calculations are not completely accurate by computers

• Intuitively, we have an ill-conditioned problem if the solution is very sensitive to the change of data values

$$\text{cond}(A) = \|A\|\cdot \|A^{-1}\|$$

💡

A singular matrix has condition number $\infty$.