14. Generative Model

Generative Model

Given training dataset, we want to generate new samples from the same distribution. 즉 Generative model은 density of the data를 추정하는 것이 목표이다.

💡

learn $p_{\text{model}}(x)$ that approximates $p_{\text{data}}(x)$

Applications of Generative Model

1. Density estimation
   1. Data exploration
   2. Anomaly detection

2. Image-to-Image translation
   1. Super-resolution : Increase the resolution
   2. Style transfer
   3. Colorization

Autoencoder for Data Generation

The decoder of AE can be used for data generation

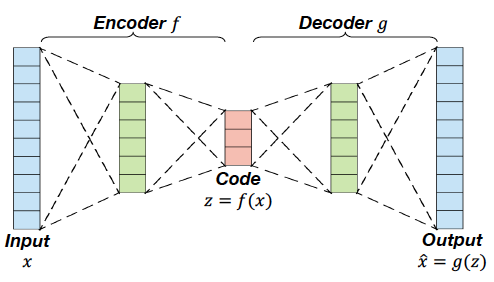
하지만 문제가 발생한다.

1. We should put a latent code

2. 하지만 우리는 plausible latent code의 distribution을 모르므로 문제가 발생한다.

이러한 측면에서 probablistic approach를 활용해야 한다.

💡

만약 $p(z|x)$를 추정할 수 있다면 해당 distribution을 바탕으로 $z$를 sampling하면 된다. 즉 데이터의 내용을 잘 반영할 수 있는 $z$가 확률적으로 선택되게 되므로 data 생성을 잘 하게 된다.

Examples of Latent Code Manipulation

Latent codes capture semantic information of image

Latent code captures domain information of images. 즉 image의 domain을 다른 domain으로 바꿀 수 있다.

Taxonomy of Generative Models

Explicit density : $p(x)$를 직접적으로 modeling

Implicit density : $p(x)$를 직접적으로 modeling하지 않음

Manifold Hypothesis

실제로 data가 분포하고 있는 manifold는 data가 놓여있는 공간보다 작을 것이라는 가정

즉 Mixture of Gaussian처럼 $p(x|z)$와 $p(z)$가 속한 distribution의 class를 가정하고, 이를 활용해서 결과적으로는 $p(x)$를 추정하고 싶은 것이다. $p(z)$를 활용해서 $z$를 샘플링하고, 샘플링된 $z$를 $p(x|z)$를 활용해서 $x$를 샘플링해주면 data generation 작업이 완료되게 된다.

Probabilistic Approach to Generative Model

목표는 likelihood를 최대로 만드는 것

$$p(x;\theta) = \int p(z)p(x|z;\theta)dz$$

💡

Data generation하기 위해서는 정확하게는 $p(z)$와 $p(x|z;\theta)$만 있으면 된다. 그걸 구하는 작업이 사실상 likelihood인 $p(x;\theta)$를 최대로 하게끔 하는 parameter를 찾는 작업과 같게 된다. 하지만, 위 상황에서 $z$가 continuous r.v인 경우 적분때문에 intractable 하다.

Variational Autoencoder(VAE)

Intractability

$$p(x;\theta) = \int p(z)p(x|z;\theta) \\ = \mathbb E_{z \sim p(z)}[p(x|z;\theta]$$

True posterior $p(z|x;theta)$를 another (encoder) network를 활용해서 approximate하고자 하는 것

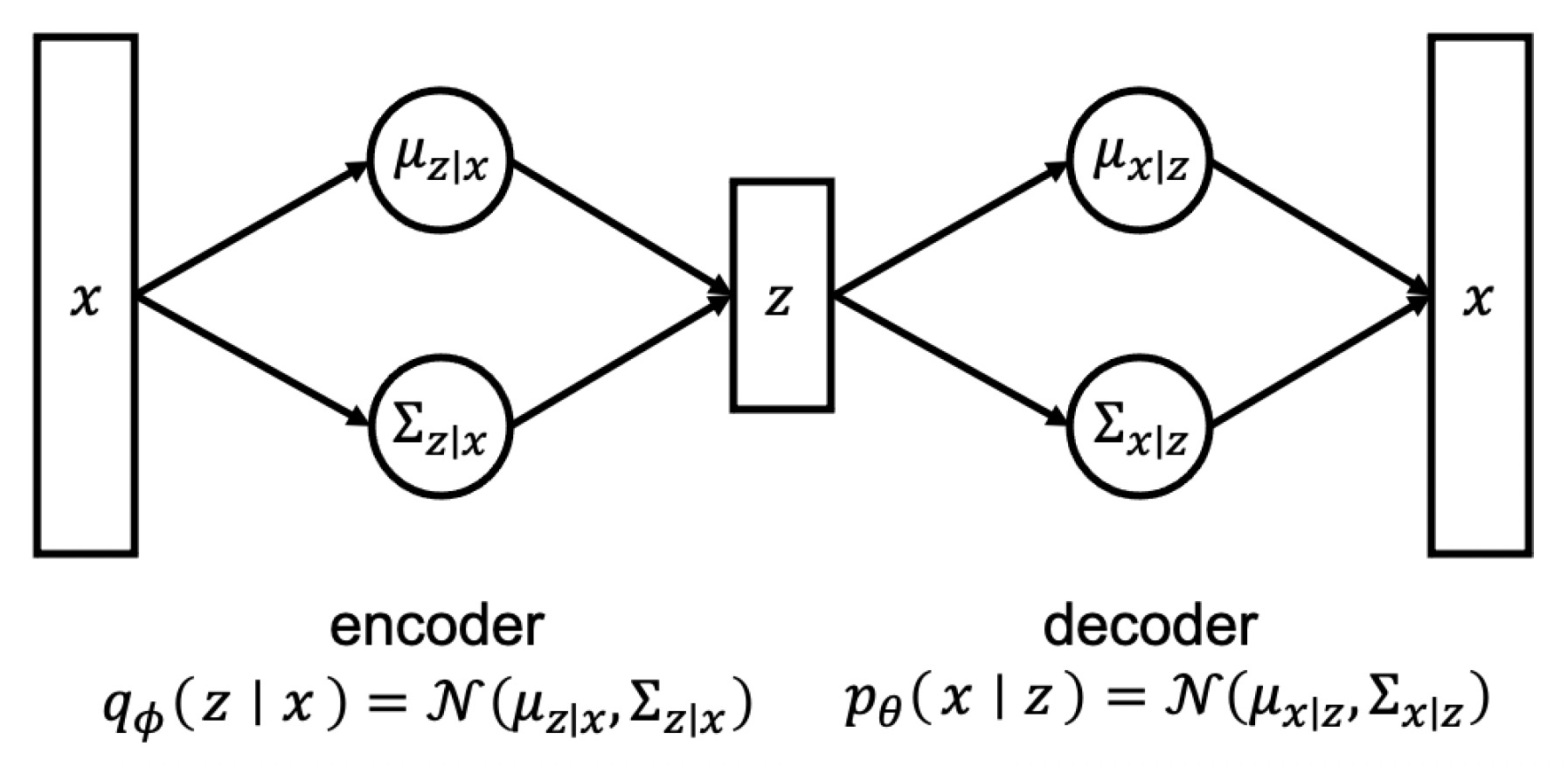
There are two neural network $f_\phi$ for encoder and $g_\theta$ for decoder

$$q_\phi(z|x) = \mathcal N(f_\phi(x)_1, (f_\phi(x)_2)^2) \\ p_\theta(x|z) = \mathcal N(g_\theta(z)_1, (g_\theta(z)_2)^2)\\ z\sim \mathcal N(0, I)$$

💡

$q_\phi(z|x)$는 $p(z|x)$를 approximate하는 것이 목적이다. 이때 $q_\phi(z|x)$를 정규분포로 고르게 된다. (즉 평균과 표준편차를 neural net으로 구한다고 생각하면 된다.)

본적으로 VAE의 목표는 주어진 입력 데이터 $x$에 대한 $p(x)$를 근사화하는 것이다. 이를 위해 VAE는 인코더 네트워크를 사용하여 입력 데이터 $x$를 잠재 변수 $z$로 인코딩하고, 디코더 네트워크를 사용하여 잠재 변수 $z$로부터 입력 데이터 $x$를 재구성합니다. 이 과정에서 $p(z)$와 $p(z|x)$ 간의 KL 발산이 최소화되도록 학습한다..

KL 발산을 최소화하는 것은 $p(z)$와 $p(z|x)$ 간의 차이를 줄이는 역할을 한다. 따라서 VAE의 훈련 과정은 잠재 변수 $z$를 샘플링하는 과정이 아닌, 입력 데이터 $x$를 기반으로 잠재 변수 $z$를 인코딩하고, 그것을 다시 디코딩하여 재구성한 결과와 원래의 입력 데이터 $x$ 간의 차이를 최소화하는 방향으로 진행된다.

이러한 접근 방식은 단순히 $p(z)$에서 $z$를 샘플링하고, 해당 $z$를 기반으로 $p(x|z)$를 통해 새로운 데이터를 생성하는 방식보다 더 성능이 좋을 수 있다. VAE는 입력 데이터 $x$의 분포를 고려하여 잠재 변수를 학습하기 때문에, 더 풍부하고 의미 있는 잠재 변수 표현을 얻을 수 있다. 이는 더 정교한 데이터 생성과 잠재 변수 공간에서의 보다 유용한 연산을 가능하게 한다.

Formula

$$\log p_\theta(x) = \int q_\phi(z|x)\log p_\theta(x)dz \\\ = \int q_\phi(z|x)\log \frac{p_{\theta}(p|z)p(z)}{p_{\theta}(z|x)}dz \\ = \int q_\phi(z|x)\log \frac{p_{\theta}(p|z)p(z)}{p_{\theta}(z|x)}\frac{q_\phi(z|x)}{q_\phi(z|x)}dz \\ = \int q_\phi(z|x)\log p_\theta(x|z)dz - KL(q_\phi(z|x)||p(z)) + KL(q_\phi(z|x)||p_\theta(z|x))\\ = \mathbb E_{z\sim q_\phi(z|x)}[\log p_\theta(x|z)] - KL(q_\phi(z|x)||p(z)) + KL(q_\phi(z|x)||p_\theta(z|x))$$

$KL(q_\phi(z|x)||p_\theta(z|x))$의 경우에는 $p_\theta(z|x)$가 어떤 distribution인지 모르기 때문에 계산하는 것이 불가능하다.

하지만, KL divergence의 값은 항상 양수이므로 해당 값은 양수라는 것은 보장할 수 있다.

ELBO

위 내용을 바탕으로 다음과 같은 부등식을 유도할 수 있다.

$$\log p_\theta(x) = \mathbb E_{z\sim q_\phi(z|x)}[\log p_\theta(x|z)] - KL(q_\phi(z|x)||p(z)) + KL(q_\phi(z|x)||p_\theta(z|x)) \\ \ge \mathbb E_{z\sim q_\phi(z|x)}[\log p_\theta(x|z)] - KL(q_\phi(z|x)||p(z))$$

이때 $E_{z\sim q_\phi(z|x)}[\log p_\theta(x|z)]$ 를 Reconstruction error 라고 부른다. 수식상 negative cross entropy이므로 $q_\phi(z|x)$와 $p_\theta(x|z)$와의 거리를 반영하고 있는 인자이다. 즉 얼마나 잘 근사했는지를 반영해주는 인자이다.

추가적으로 $KL(q_\phi(z|x)||p(z))$를 Regularization error 라고 부른다. 즉 posterior와 prior가 최대한 비슷하게끔 하는 인자라고 생각해주면 된다.

💡

애초에 Regularization error에서 볼 수 있는 것처럼 posterior와 prior와의 차이를 고려하고 있기 때문에, 실제 data generation 단계에서는 $z$를 $\mathcal N(0, I)$에서 sampling해주면 된다.

결과적으로

$$\text{ELBO}= \mathcal L(x,\phi, \theta) := \mathbb E_{z\sim q_\phi(z|x)}[\log p_\theta(x|z)] - KL(q_\phi(z|x)||p(z))$$

라고 정의하게 된다.

💡

ELBO는 Variational lower bound라고 불린다.

그리고 우리는 직접적으로 likelihood인 $p_\theta(x)$를 최대화시키는 것이 아니라 ELBO 를 최대로 만들게끔 하는 parameter를 찾는 것이 목표이다.

💡

이 과정에서 오차가 발생하지만, $p(x|z)$의 untractable때문에 감수해야 한다.

Training VAE

위의 내용을 바탕으로 VAE의 objective는 다음과 같다

$$\argmax_{\phi, \theta}\sum_{i = 1}^N \mathcal L(x^{(i)}, \theta, \phi) \\ = \argmax_{\phi, \theta}\sum_{i = 1}^N \mathbb E_{z\sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)}|z)] - KL(q_\phi(z|x^{(i)})||p(z))$$

$\mathbb E_{z\sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)}|z)]$의 경우에는 analytic solution 이 존재하지 않는다. 애초에 $p_\theta(x|z)$가 어떤 함수인지조차 모른다.

그래서 해당 expectation값을 Monte-Carlo Method를 통해 근사시킨다.

$$\mathbb E_{z\sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)}|z)] \approx \frac{1}{N}\sum_{n = 1}^N\log p_\theta(x|z^{(n)}) \\ = - \log\sigma_x^2\sqrt{2\pi}-\frac{1}{2N}\sum_{n = 1}^N\frac{(x-g_\theta(z^{(n)})^2}{\sigma_x^2}$$

where $z^{(1)}, \dots, z^{(N)}$ are samples drawn from $q_\phi(z|x)$

💡

일종의 empirical distribution 취급해준 것이라고 이해하면 된다.

하지만, 치명적인 단점이 있는데 sampling을 하는 과정에서 $q_\phi(z|x^{(i)})$에 대한 term이 사라진 것이다. 이렇게 되면 back-propagation 과정에서 parameter를 업데이트하지 못하게 된다. 따라서 Reparameterization 을 통해 해당 문제를 해결하게 된다.

• What is the reparameterization trick?

  Some random variables can be represented as a function of another variable

즉, 다음과 같이 reparameterization을 수행한다.

$$z^{(i)} = \sigma\epsilon^{(i)} + \mu \\ \Rightarrow z^{(i)} = f_\phi(x^{(i)})_2\epsilon^{(i)} + f_\phi(x^{(i)})_1\\\text{where }\epsilon^{(i)} \sim \mathcal N(0, 1)$$

Therefore

$$\mathbb E_{z\sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)}|z)] \approx \frac{1}{N}\sum_{n = 1}^N\log p_\theta(x|z^{(n)}) \\ = - \log\sigma_x^2\sqrt{2\pi}-\frac{1}{2N}\sum_{n = 1}^N\frac{(x-g_\theta(z^{(n)})^2}{\sigma_x^2} \\ = - \log\sigma_x^2\sqrt{2\pi}-\frac{1}{2N}\sum_{n = 1}^N\frac{(x-g_\theta(f_\phi(x^{(i)})_2\epsilon^{(i)} + f_\phi(x^{(i)})_1))^2}{\sigma_x^2}$$

이렇게 되면 미분을 정상적으로 수행할 수 있게 된다.

$KL(q_\phi(z|x^{(i)})||p(z))$의 경우에는 analytic solution이 존재한다.

$$\int q_\phi(z|x)\log p(z) dz = \int \mathcal N(z;\mu, \sigma^2)\log \mathcal N(z;0, I) dz \\ = -\frac{J}{2}\log 2\pi - \frac{1}{2}\sum_{j = 1}^J(u_j^2+\sigma_j^2) \\ \text{where } J \text{ is a dimensionality of }z$$

즉 $\mu$와 $\sigma$에 대해서 미분할 수 있다.

요약하면 다음과 같다.

$$\log p_\theta (x) \ge \mathcal L(x,\phi, \theta) \\ = \mathbb E_{z\sim q_\phi(z|x)}[\log p_\theta(x|z)] - KL(q_\phi(z|x)||p(z)) \\ \approx \frac{1}{N}\sum_{n = 1}^N\log p_\theta(x|z^{(n)})- KL(q_\phi(z|x)||p(z^{(n)}))$$

💡

여기서 expectation은 Monte Carlo method에 의해서 근사되고, decoder $\theta$에 대해서 derivative를 구하는데 있어서는 단지 주어지게 되지만 encoder $\phi$에 대해서 derivative를 구하기 위해서는 reparameterization trick을 sampling operation에서 $\phi$의 dependency를 얻을 수 있는 곳에 사용해야 한다. 그러면 $\phi$에 대해서 derivative를 구하는 것이 가능해진다.

Pros and Cons of VAE

장점

1. Density의 explicit estimation으로서 여러 trick을 사용하더라도 어찌됐든 probability를 구할 수 있기 때문에 이를 principled approach라고 부를 수 있다

2. Encoder가 다른 용도로 활용할 수 있다. (ex : semi-supervised learning)

단점

1. Approximate했다는 점에서는 한계를 지닌다

2. GAN에 비해서 blurry하고 quality가 낮다.

VAE(Variational AutoEncoder)

gaussian37's blog

https://gaussian37.github.io/dl-concept-vae/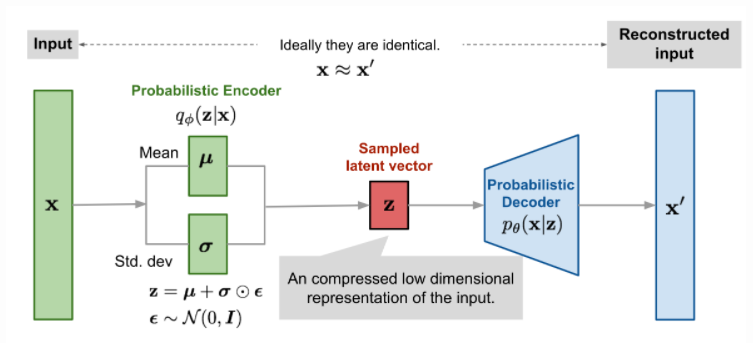

Generative Adversarial Network

앞서 살펴본 것처럼 VAE는 실제 data의 distribution을 학습하기 위해서 우선 data를 latent space에 encoding하고 그것을 다시 data space에 대응시키는 작업을 거치게 된다. 이 과정에서 Latent space 상에서의 distribution을 학습하게 되는데 이 과정에서 굉장한 non-trivial summation을 감행하게 된다.

💡

Likelihood를 정의하고 이를 통해 모델을 학습한다는 점에서는 학습의 정확성을 올릴 수는 있으나, 이로 인해 계산의 복잡성을 증가시키는 단점이 있다.

이와 반대로 GAN은 간단한 distribution으로부터 data space을 대응시키는 transformation 을 학습하는 것을 목표로 두고 있다. 즉 바로 latent variable $z$를 바로 $x$로 변환하는 것을 시도하는 것이다.

Training GAN : Two-Player Game

이를 위해서 2가지 Network를 정의한다.

Discriminator network D : Tires to distinguish between real and fake images

💡

출력값이 1이면 real이라고 판단하는 것이고, 0이면 fake라고 판단하는 것이다.

Generator network G : Tires to fool the discriminator by generating real-looking images

💡

즉, Discriminator는 진짜와 가짜를 잘 구분하는 것을 학습하는 것을 목표로 두고, Generator는 진짜 같은 사진을 학습하는 것을 목표로 두고 있다. 즉 일종의 치킨게임같은 느낌이다.

이러한 의미에서 GAN의 학습은 minmax game 에 해당한다.

$$\min_\theta\max_\phi\mathbb E_{x\sim p_\text{data}}\log(D_\phi(x)) + \mathbb E_{z\sim p(z)}\log(1-D_\phi(G_\theta(z)))$$

Discriminator $\phi$ perspective

1. Discriminator 입장에서는 진짜 데이터들에 해당하는 $x$에 대해서는 real이라고 판단하고 싶어할 것이다. 즉 $\mathbb E_{x\sim p_{\text{data}}}\log (D_\phi(x))$가 커지면 좋은 상황이다. (1이 나올수록 좋은 상황이므로)

2. 반대로 가짜 데이터인 $G_\theta(z)$에 대해서는 fake라고 판단하고 싶어할 것이다. 즉 $E_{z\sim p(z)}\log(1-D_\phi(G_\theta(z)))$가 커지면 좋은 상황이다. (Discriminator의 값이 작아질수록 해당 값이 커진다.)

Gradient ascent on the discriminator

$$\max_\phi\mathbb E_{x\sim p_\text{data}}\log(D_\phi(x)) + \mathbb E_{z\sim p(z)}\log(1-D_\phi(G_\theta(z)))$$

Generator $\theta$ perspective

1. 반대로 Generator 입장에서는 가짜 데이터임에도 불구하고 Discriminator가 1이라고 판단했으면 좋겠는 상황이다. 즉 $E_{z\sim p(z)}\log(1-D_\phi(G_\theta(z)))$가 작아지면 좋은 상황이다.

Gradient descent on generator

$$\min_\theta \mathbb E_{z\sim p(z)}\log(1-D_\phi(G_\theta(z)))$$

Training GAN : Improving Convergence

하지만 Generator의 성능이 Discriminator보다 좋지 않은 경우, gradient가 거의 0으로 수렴하는 문제가 발생한다.

💡

일반적으로 Generator가 Discriminator보다 훨씬 더 어려운 task이므로 해당 문제는 더욱 가속화된다.

따라서 $\log(1-D_\phi(G_\theta(z)))$를 작게 하는 것이 아닌 $\log(-D_\phi(G_\theta(z)))$를 작게한다.

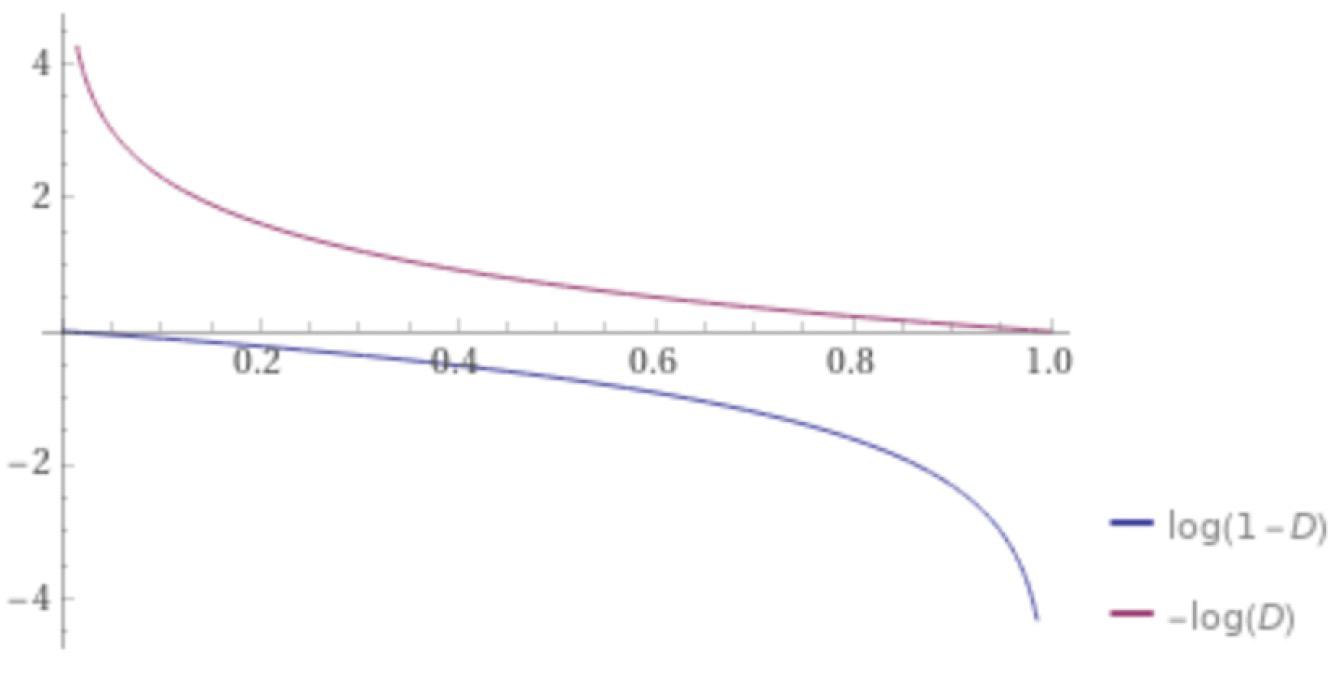
→ Generator가 Discriminator에 비해서 학습이 잘 안되었다는 말은 $D\phi(G_\theta(z)$가 거의 항상 0으로 판단을 한다는 것이다. 이때 $\log(1-D_\phi(G_\theta(z)))$의 그래프를 보게 되면 gradient가 거의 0이다. 즉 학습이 잘 되지 않는다. 따라서 $\log(-D_\phi(G_\theta(z))$를 최소화하는 방식으로 Generator가 학습하는 식으로 변경하게 되면 조금 더 나은 수렴가능성을 보장할 수 있게 된다.

Algorithm

Generating Data from GAN

학습을 마치고 data generate 단계에서는 Generator만 사용하게 된다.

$$\text{new data} = G_\theta(z) \\ \text{where }z \sim p(z)$$

Example of GAM

Issues

Non-convergence

Mode Collapse

특정한 소수의 data class에만 괜찮은 결과를 generator가 생성함으로써 discriminator를 속이는 문제이다.

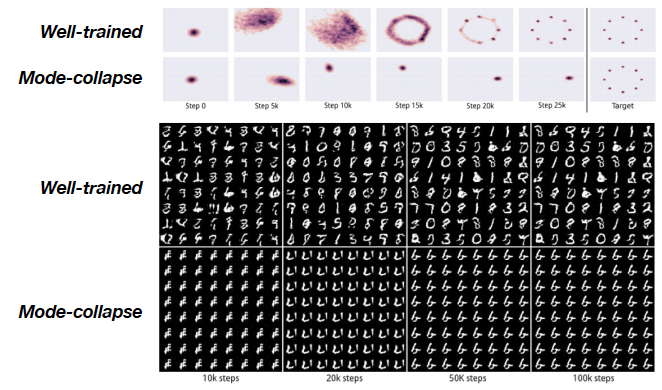
Mode collapse is a common problem that can occur when training Generative Adversarial Networks (GANs). In essence, it's when the generator network learns to fool the discriminator by producing a limited range of outputs—often just a single point or a small cluster of point-ignoring the complexity and diversity of the real data distribution. When mode collapse occurs, the GAN fails to generate diverse samples, instead repeatedly outputting very similar or even identical samples.

이러한 문제는 Mini-batch Trick 을 사용하면 피할 수 있다.

1. Real image와 Generated image를 discriminator에 다른 batch로 넣는다.

   이 과정에서 similarity 의 정도를 계산하고 해당 값은 discriminator의 input으로 주어진다.

2. 만약 Mode collapse가 발생하게 되면 Generated image의 similarity score가 굉장히 크게 올라갈 것이다. 이에 대한 penalty를 주면 된다.