11. Clustering and K-means Algorithm
- -
Unsupervised Learning
Clustering
- K-means algorithm
- Mixture of Gaussian
Dimensionality reduction
- Principal component analysis (PCA)
- Factor analysis
- Mixture of Factor analysis
- Kernel PCA
- t-SNE
Generative model
- Generative adversarial networks (GAN)
- Variational Auto Encoder (VAE)
Different definitions of likelihood
Let's break down the likelihood functions for generative and discriminative models in both supervised and unsupervised contexts:
1. Generative Models:
Generative models aim to learn the joint probability distribution P(x,y) in the supervised learning or P(x) in unsupervised learning. They model the way the data is generated by learning P(x,y)=P(x∣y)P(y) for supervised learning or just P(x) for unsupervised learning.
Supervised Learning:
In the case of a generative model in supervised learning, the likelihood function would be defined based on the joint probability distribution of both the input data and the labels, P(x,y). Given a dataset D={(x1,y1),(x2,y2),...,(xn,yn)} and a model with parameters θ, the likelihood function L(θ;D) could be expressed as:
This is the product of the probabilities of each (xᵢ,yᵢ) pair under the model with parameters θ.
Unsupervised Learning:
In unsupervised learning, generative models aim to learn the distribution P(x). Given a dataset D={x1,x2,...,xn} and a model with parameters θ, the likelihood function L(θ;D) could be expressed as:
This is the product of the probabilities of each xᵢ under the model with parameters θ.
2. Discriminative Models:
Discriminative models aim to learn the conditional probability distribution P(y∣x) in supervised learning. They model the boundary between classes rather than the distribution of individual classes.
Supervised Learning:
In the case of a discriminative model in supervised learning, the likelihood function would be defined based on the conditional probability of the labels given the input data, P(y∣x). Given a dataset D={(x1,y1),(x2,y2),...,(xn,yn)} and a model with parameters θ, the likelihood function L(θ;D) could be expressed as:
This is the product of the probabilities of each yi given xi under the model with parameters θ.
Unsupervised Learning:
In unsupervised learning, the concept of discriminative models doesn't directly apply because there are no labels y to condition upon. Hence, we don't typically discuss discriminative models in the context of unsupervised learning.
These formulas are based on the assumption that the data points are independently and identically distributed (i.i.d.). In real-world scenarios, these assumptions might need to be modified based on the specifics of the data and the model.
How can we generate new data?
In a generative model, once we have learned the distributions P(x∣y;θ) and P(y;θ), we can use them to generate new data instances. Here's how that process works:
- Sample a class label: We start by
samplinga class label from the distribution P(y;θ). This distribution gives us the probability of each class label, and we can sample from it to get a class label. For example, if we're working with a binary classification problem, P(y;θ) might tell us that the probability of class 0 is 0.6 and the probability of class 1 is 0.4. We can then sample from this distribution to get a class label. Let's say we sample and get the class label y = 0.
- Sample a data instance: Once we have a class label, we can
samplea data instance from the distribution P(x∣y;θ). This distribution gives us the probability of different data instances given a certain class label. So in our example, we would sample a data instance from the distribution P(x∣y=0;θ). This gives us a data instance that is likely under class 0 according to our model.
By doing this, we have generated a new (x,y) pair. The x is generated in a way that is likely under the class y, so the (x,y) pair should be similar to the ones the model was trained on. If we repeat this process, we can generate as many new (x,y) pairs as we want.
Clustering
Unlabeled data points를 여러 group으로 partitioning하는 것
similarity 일 수도 있고, distance 일 수도 있다.Non-parametric approach
K-means clustering
Soft K-means clustering
Parametric approach
Mixture of Gaussian (Generative model로 볼 수도 있음)
K-means Algorithm
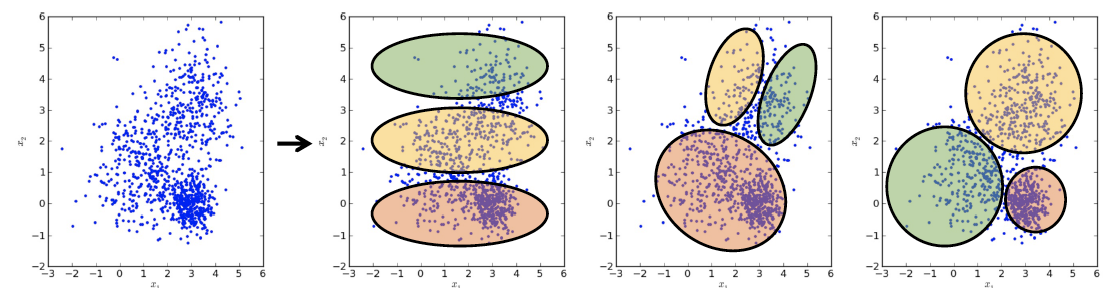
어느 것이 더 좋은지 판단하기 위해서는 criterion이 필요하다.
거리 를 기준으로 cluster를 형성하고 싶은 것이다.이때, N개의 data point {xi}i=1N(xi∈RD)가 있고, 이러한 데이터들을 K개의 cluster로 나누려고 한다고 가정하자.
where zi={zik}k=1K are the assignment variables for the i-th data point. μ={μk}k=1K are the center of K clusters
Procedure
- μ 를 랜덤하게 선택한다. (i.e. K개의 cluster의 중심을 랜덤으로 설정한다.)
- Assignment step : Given μ, find the optimal assignment variables zzik={10if k=argmink∥xi−μk∥2otherwise💡즉 주어진 cluster의 중심으로부터 가장 가까운 cluster에 할당하는 작업이라고 이해해주면 된다.
- Update step : Given z, find the optimal centroids μμk=∑izik∑izikxi💡즉, cluster에 속한 것끼리만 평균을 취해서 새로운 centroid를 계산하는 것이다.💡위 식은 J를 μk에 대해서 미분하고 0이되는 값을 구한 결과이다.
Always converges?
The cost function is guaranteed to decrease monotonically in each iteration because the data points are always assigned to the closest centroid. This means that the distance between each data point and its assigned centroid is always decreasing. As a result, the cost function, which is the sum of the squared distances between each data point and its assigned centroid, is also guaranteed to decrease monotonically.
→ 귀류법으로 증명할 수 있음
→ 만약에 커진다고 가정하면 모순이 나옴. (애초에 최소가 되게끔하는 방향으로 centroid가 움직이므로)
The K-means algorithm does not always converge to the global minimum because the initial choice of centroids can affect the final clustering. If the initial choice of centroids is not representative of the data, the algorithm may converge to a local minimum that is not the global minimum.
Properties
- Local optimum is found
- Convergence is guaranteed in a finite number of iteration
- Computational complexity per iteration
- Assignment step : O(KND) D는 data의 dimension💡모든 data N개에 대해서, 존재하는 모든 cluster K개의 centroid와의 거리를 비교해야하기 때문이다. 추가적으로 data space가 RD라고 가정해서 추가로 D만큼의 시간복잡도가 들어가는 것이다.
- Update step : O(N)
- Assignment step : O(KND) D는 data의 dimension
Limitations
- 초기 centroid에 민감함
→ 좀 더 이 부분에 robust한 모델이 K-means++
💡앞서 살펴본 것처럼 초기 centroid 설정에 따라서 global optima에 도달할 수 있는 지 여부가 달라지게 된다.
- Outlier에 민감함

→ 좀 더 이 부분에 robust한 모델이
K-medoids(centroids as the actual data points)💡해당 부분은 과제에 나왔으므로 주의하도록 하자.
- The shape of each cluster is always convex
→ Convex hull을 그려봤을 때 convex가 그려짐
Soft K-means Algorithm
소중한 공감 감사합니다


