6. Generative Learning Algorithm

Discriminative vs Generative Learning

Discriminative learning : How do I separate the classes

Estimate parameters of decision boundary directly from labeled examples.

→ We can make model $p(y|x)$ directly by using datasets

Generative learning : What does each class look like

Model the distribution of inputs characteristic of the class

→ Ultimately, we want to find $p(y|x, \theta)$ (If supervised learning)

But, in generative learning, we want to find it by modeling $p(x|y)$ and $p(y)$ ($p(y)$ : class prior)

$$\argmax_yp(y|x) = \argmax_y\frac{p(x|y)p(y)}{p(x)} \\ = \argmax_y p(x|y)p(y)$$

Likelihood for Discriminative learning

$$\mathcal L(\theta;\mathcal D) = \prod_{i = 1}^m p(y^{(i)}|x^{(i)};\theta)$$

Likelihood for Generative learning

$$\mathcal L(\theta;\mathcal D) = \prod_{i = 1}^m p(x^{(i)}, y^{(i)};\theta) \\ = \prod_{i = 1}^m p(x^{(i)}|y^{(i)};\theta)p(y^{(i)};\theta)$$

💡

Discriminative learning과 Generative learning의 cost function이 다름을 매우 주의해야 한다.

Gaussian Discriminant Analysis (GDA) : continuous-value case

가우시안 분포와 분별 함수 (선형 분별 분석(LDA), 2차 분별 분석(QDA))

gaussian37's blog

https://gaussian37.github.io/ml-concept-gaussian_discriminant/

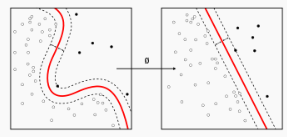
• Condition for use GDA

  x : continuous-valued random variables일 때 GDA 사용가능

It models $p(y)$ and $p(x|y)$ using Bernoulli and a multivariable Gaussian respectively.

• Class prior : $y$ ~ Bernoulli$(\phi)$

  $$p(y) = \phi^y (1-\phi)^{1-y}$$

• Class-conditional distribution : Multivariable Gaussian

  $$p(x|y = 0)= \frac{1}{(2\pi)^{d/2}|\sum|^{1/2}}exp(-\frac{1}{2}(x-\mu_o)^T{\sum}^{-1}(x-\mu_0)) \\ p(x|y = 1)= \frac{1}{(2\pi)^{d/2}|\sum|^{1/2}}exp(-\frac{1}{2}(x-\mu_1)^T{\sum}^{-1}(x-\mu_1))$$

(Mathematical simplicity때문에 covariance matrix가 동일하다고 가정. Mean만 다름. 즉 평행이동적 관점)

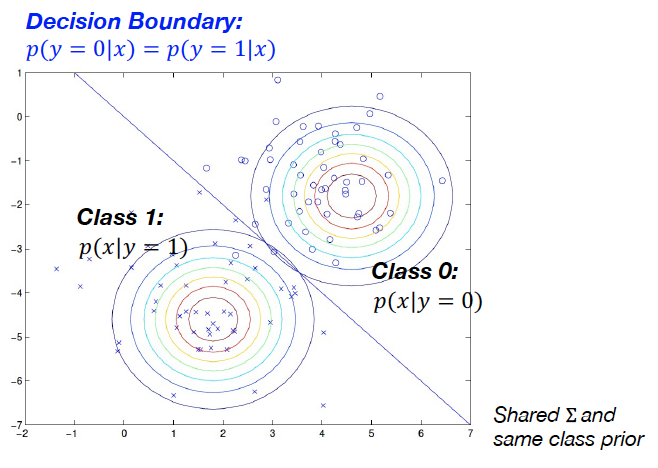
GDA의 목적이 f(y|x) 즉 distribution을 구하고 싶은 것!

→ 즉, 각각의 클래스에 들어갈 확률을 구하고 싶은 것!

Discriminantive learning의 경우는 직접적으로 바로 해당 class에 들어갈 확률을 도출함

→ 반면 generative learning의 경우에는 그렇게 하지 않음

만약 covariance matrix가 서로 다른 경우라면?

It has a quadratic function in x, so the decision boundary is a conic section

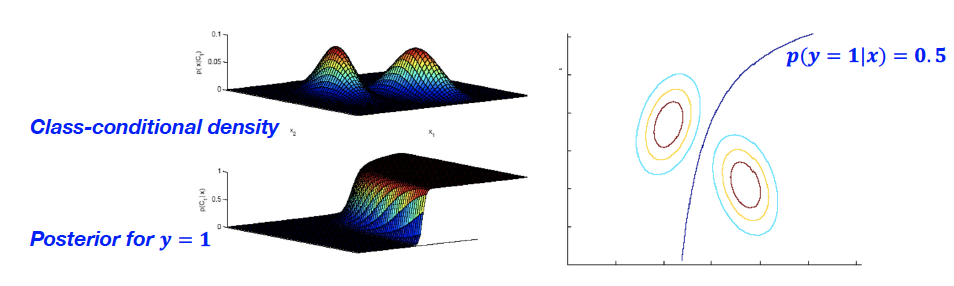
GDA vs Logistic Regression

The quantity $p(y = 1 | x, \phi, \sum, \mu_0, \mu_1)$ can be expressed as a function of $x$

$$p(y = 1 | x, \phi, \sum, \mu_0, \mu_1) = \frac{1}{1 + exp(-w^Tx + b)}$$

→ 역은 성립하지 않음

GDA makes a stronger Assumption : class-conditional density is Gaussian

→ GDA is more data efficient when the modeling assumptions are correct or at least approximately correct

즉, 예상이 맞는다면 데이터가 적어도 잘 먹힘.

Logistic regression makes weaker assumptions

→ When the data is indeed non-Gaussian, logistic regression will almost always do better than GDA.

→ more robust to deviations from modeling assumptions.

Naive Bayes : discrete-value case

Naive Bayes’ assumes that $\forall i \ne j, x_i$ and $x_j$ are conditionally independent given y

💡

Conditionally independent is different from independent

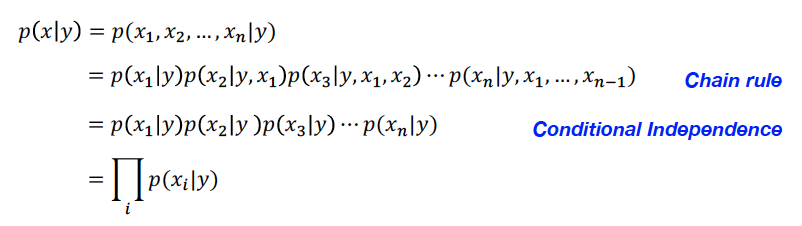
여기서 $x$가 n-dimensional이라고 생각해주면 됨. 즉, feature이 총 n개가 있고, 각각의 feature별로 $x_i$가 되는 확률이랑 연관되어있는 것

Parameters

$$\phi_{i|y = 1} = p(x_i = 1| y = 1) \\ \phi_{i|y = 1} = p(x_i = 1| y = 1) \\ \phi_y = p(y = 1)$$

Log-likelihood

$$\mathcal L(\phi_y, \phi_{j|y = 0}, \phi_{j|y = 1}) = \prod_{i = 1}^mp(x^{(i)}, y^{(j)})$$

Naive Bayes Classifier

데이터들을 이용해서 $\pi_k$ and $\theta_{ijk}$ 를 추정

$$y^{new} = \argmax_{y_k}\pi_k \prod_i \theta_{ijk} \text{ where }x_{ij} = x_i^{new}$$

Subtlety of Naive Bayes

만약 데이터에 $x_{ij}$가 없으면 $\theta_{ijk}$가 0이 될 수 있다. (Unseen feature problem)

해결 방법

1. Laplace smoothing

2. MAP estimate with prior

Laplace Smoothing

적어도 1번 일어나게끔 보정

→ 단순히 1씩 더하는 것이 아니라 prior에 의해서 0이 되지 않게끔 조정하는 것도 가능하다.

Example

• 어떻게 text를 representation할 것인가

  

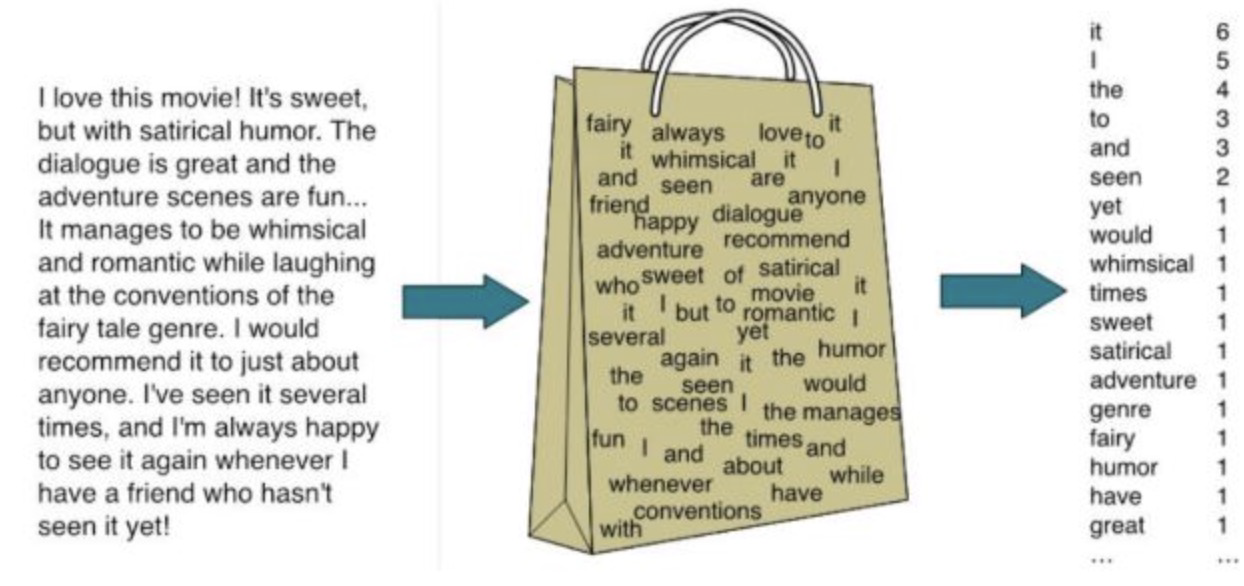
  → Back-of-Words

  단, 이렇게 될 경우에는 sequential order가 무시된다는 단점이 존재한다. 단순히 빈도만 고려하므로.

  각 단어마다 1개의 dimension으로 취급된다.

• 어떻게 각 단어의 단어의 class conditional probability를 구할 것인가?

$|V|$ : dictionary의 cardinality

$w$ : 해당 단어