11. Penalty and Barrier Methods

Introduction

In the last article, we discussed the use of feasible-point methods for solving constrained optimization problems. These methods are based on minimizing the Lagrangian function while attempting to attain and maintain feasibility. When inequality constraints are present, these methods solve a sequence of subproblems with a changing active set until a solution to the original constrained problem is found.

However, there are some major disadvantages to this approach.

1. As the number of constraints increases, the number of potential subproblems.

2. The idea of keeping the constraints satisfied exactly, although easily achieved in the case of linear constraints, is much more difficult to accomplish in the case of nonlinear constraints.

Some of these disadvantages can be removed by using penalization methods. These methods solve a constrained optimization problem by solving a sequence of unconstrained optimization problems. The hope is that in the limit, the solutions of the unconstrained problems will converge to the solution of the constrained problem.

In contrast to active-set methods, this approach takes into account all constraints, and thus the difficulties of guessing a correct active set are avoided. Further, since penalization techniques don’t attempt to keep the constraints satisfied exactly, they can be more suitable for handling non-linear constraints.

Although penalization methods ameliorate some of the difficulties, they introduce difficulties of their own. In particular, it can give rise to ill-conditioning problems.

Classical Penalty and Barrier Methods

The general class of penalization methods includes two groups of methods:

1. penalty methods: imposes a penalty for violating a constraint

2. barrier methods: imposes a penalty for reaching the boundary of an inequality constraint

Suppose that our problem is given in the form:

$$\min f(x)$$

$\text{subject to}$

$$x\in S$$

where $S$ is the set of feasible points.

Define

$$\sigma(x) = \begin{cases}0 \quad \text{if } x\in S \\ \infty \quad \text{if }x\notin S\end{cases}$$

The function $\sigma$ can be considered as an infinite penalty for violating feasibility. Hence the constrained problem can be transformed into an equivalent unconstrained problem in the form:

$$\min f(x) + \sigma(x)$$

💡

즉, violating constraint하는 영역에 대해 함숫값을 무한대로 만들어버림으로써 간접적으로 이를 해결하는 것으로 기하학적인 이해를 할 수 있다.

However, this is not a practical idea, since the objective function of the unconstrained minimization is not defined outside the feasible region. Moreover, it makes a discontinuities within the boundaries.

Therefore, barrier and penalty methods solve a sequence of unconstrained subproblems that are more manageable, and that gradually approximate the infinite penalty function.

Barrier Methods

Consider the nonlinear inequality constrained problem

$$\min f(x)$$

$\text{subject to}$

$$g_i(x) \ge 0, i = 1, \dots, m$$

Barrier methods use a barrier term that approaches the infinite penalty function $\sigma$. Let $\phi(x)$ be a function that is continuous on the interior of the feasible set, and that becomes unbounded as the boundary of the set is approached from its interior:

$$\phi(x) \to \infty \quad \text{as} \quad g_i(x) \to 0$$

There are two examples:

1. Logarithmic function

   $$\phi(x) = - \sum_{i = 1}^m \log(g_i(x))$$

2. Inverse function

   $$\phi(x) = \sum_{i = 1}^m \frac{1}{g_i(x)}$$

Now let $\mu$ be a positive scalar. Then $\mu\phi(x)$ will approach $\sigma(x)$ as $\mu$ approaches zero.

By adding a barrier term of the form $\mu\phi(x)$ to the objective, we obtain a barrier function

$$\beta_\mu(x) = f(x) + \mu\phi(x)$$

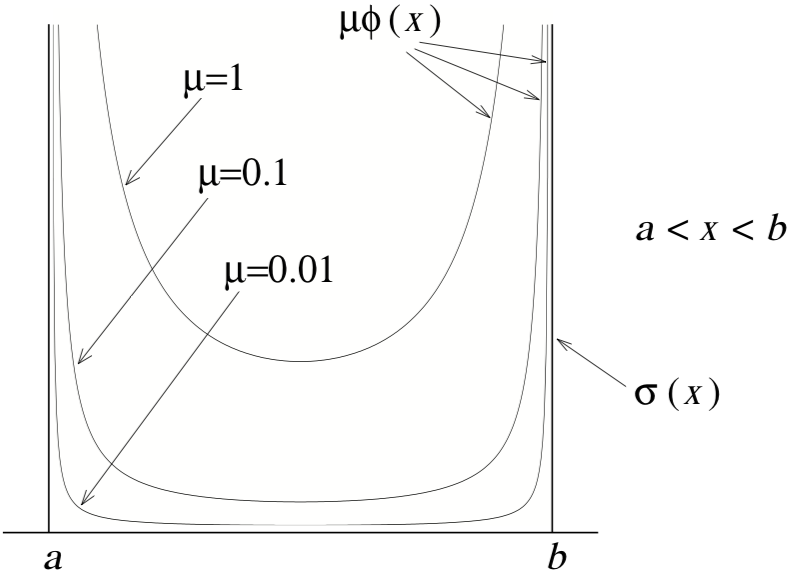
where $\mu$ is referred to as the barrier parameter

Barrier methods solve a sequence of unconstrained minimization problem of the form

$$\min_x \beta_{\mu_k}(x)$$

for a sequence $\{\mu_k\}$ of positive barrier parameters that decrease monotonically to zero.

💡

계속해서 barrier parameter를 줄이는 이유는 effect of the barrier term를 줄이기 위함이다. 이를 통해 점진적으로 boundary에 존재하는 feasible region에 접근할 수 있도록 한다.

Why solve a sequence of problems? The reason is that when the barrier parameter is small, the discontinuous at $a$ and $b$ makes a problem. For this reason we start with larger values of the barrier parameter. If $\mu$ is decreased gradually, and if the solution of one unconstrained problem is used as the starting point of the next problem, these unconstrained minimization problems tend to be much easier to solve.

💡

objective function의 minimum value가 $\mu$가 작아짐에 따라서 작아진다. 특정 임계점 이하로 변동하게 될 경우 $\mu_k$의 update를 멈추면 된다.

Penalty Methods

In contrast to barrier methods, penalty methods solve a sequence of unconstrained optimization problems whose solution is usually infeasible to the original constrained problem.

An advantage of penalty methods is that they don’t require the iterates to be strictly feasible. Thus, unlike barrier methods, they are suitable for problems with equality constraints.

💡

Equality constraint의 경우에는 barrier method로 풀기에 적합하지는 않다. 잘 생각해보면 해당 constraint를 제외하고는 무한대로 설정되기 때문이다.

Consider the equality constraint problem

$$\min f(x)$$

$\text{subject to}$

$$g(x) = 0$$

where $g(x)$ is a $m$-dimensional vector whose $i$’th component is $g_i(x)$

The penalty for constraint violation will be a continuous function $\psi$

$$\psi(x) = \begin{cases}0 \quad \text{if } x\in S \\ >0 \quad \text{if }x\notin S\end{cases}$$

There are two examples:

1. $l_2$ loss function

$$\psi(x) = \frac{1}{2}\sum_{i = 1}^m g_i(x)^2$$

2. Another penalty funciton

   $$\psi(x) = \frac{1}{\gamma}\sum_{i = 1}^m |g_i(x)|^\gamma$$

   where $\gamma \ge 1$

The weight of the penalty is controlled by a positive penalty parameter $\rho$. As $\rho$ increases, the function $\rho\psi$ approaches to $\sigma$. We can define the penalty function as follows

$$\pi_\rho(x) = f(x) + \rho\psi(x)$$

The penalty method consists of solving a sequence of unconstrained minimization problems of the form

$$\min \pi_{\rho_k}(x)$$

for an increasing sequence $\{\rho_k\}$ of positive values tending to infinity.

💡

More convenient than barrier methods since there is no need of an initial feasible point.

However, it also has a problem

1. same numerical issue as for barrier method when $\rho$ is increased.

2. $f$ may be undefined for infeasible point (e.g. square root of a negative number)

What about inequality problem? Think about this case

$$\min f(x)$$

$\text{subject to}$

$$g_i(x) \le b_i, \forall i$$

In this case, we can use the penalty function by using

$$\min f(x) + \sum_i \max(0, g_i(x) - b_i)^2$$

If

$$g_i(x) \ge b_i$$

, the penalty value is 0.

However, if

$$g_i(x) < b_i$$

, the penalty value is greater than 0.

💡

Check : 2106 7th problem