3. Arithmetic for Computers

Subtraction in Hardware

Option 1 : Direct subtraction

일반적으로 잘 사용하지 않음.

→ - 연산을 실제로 구현해야하므로

Option 2 : two’s complement

Subtraction을 addition과 구분하지 않아도 됨

→ 수학적 연산의 수가 최대한 줄어야 하드웨어를 구현하는데 필요한 cost가 기하급수적으로 줄음

→ 더한 결과의 sign-bit가 알아서 조절된다는 측면에서는 유리

Overflow

빼고 더하고 하다보면 숫자를 저장할 수 있는 비트의 수가 제한되어 있기 때문에 발생하는 문제 (하드웨어의 한계로 인해서 발생)

• 정의가 무엇인가?

  Occur when the result from an operation can’t be represented with the available hardware

주의 : 5페이지 (In our case, a 32-bit word 라고 수정해야 함.

• 언제 overflow가 절대로 발생하지 않는가.

  1. 서로 다른 부호의 수를 더하는 경우

  2. 사실 같은 부호의 수를 빼는 경우 (사실상 1번 케이스와 동치)

Detecting Overflow

사실 overflow를 파악하는 가장 쉬운 방법은 sign bit가 예상된 값이 나왔는지 판단해주면 된다.

Multiplication

$$Multiplicand * Multiplier = Product$$

반드시 암기!

1. Multiplicand를 맨 위에 쓰고

2. Multiplier를 뒤에서부터 1개씩 보고 곱한다.

3. 쭉 더하고 carry 처리

→ Multiplier가 1이면 multiplicand를 그대로 쓰고, 아니면 0으로 도배한다는 규칙이 있음

Sequential Multiplication

multiplicand가 있는 영역을 64bit로 잡고, 초기값을 오른쪽에다가 둔다. multiplier가 있는 영역은 32bit로 잡고, result가 들어가는 영역은 64bit로 잡는다. multiplier의 가장 오른쪽에 있는 값이 1이면 multiplicand를 result와 더해서 result에다가 저장한다. 추가적으로 multiplicand가 있는 영역을 왼쪽으로 shit, multiplier는 오른쪽으로 shift한다.

→ 이러한 과정을 총 32번 반복한다.

Faster Multiplication

하드웨어 입장에서 빠르게 한다는 것은 의존성이 없는 연산을 동시에 처리해주면 됨

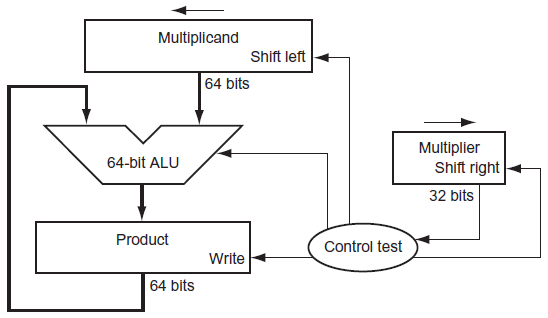
Product라고 적혀져 있는 곳 왼쪽에 product와 multiplier가 오른쪽에 존재함.

→ 논리적으로 잘 생각해보면 multiplier가 필요한 영역은 1개의 비트씩 줄고, product가 필요한 영역은 1개의 비트씩 증가하므로 이렇게 처리해도 괜찮음.

→ multiplicand 상위 32개에만 계속 더해주면 된다. (multiplicand를 shit하는 효과와 완전히 동일하게 처리할 수 있다.)

→ 1번 계산이 끝날때마다 product를 오른쪽으로 shift

→ 이러한 과정을 총 32번 반복

Parallel multiplier adder tree

사실 진정한 의미의 faster multiplication

$\log_2 32$ cycle안에 처리 가능

Multiplication in MIPS

Multiplication과 division에 한정해서 쓰이는 레지스터 : Hi, Lo

Hi 레지스터에 상위 32개의 결과가 저장되고, Lo 레지스터에 하위 32개의 결과가 저장된다.

• Multiply (mult) : signed integer

• Multiply unsigned (multu) : unsigned integer

단, Hi와 Lo는 프로그래머가 접근할 수 없는 레지스터이다. 그래서 데이터를 옮겨야하는 문제가 발생. 그래서 해당 값을 레지스터를 읽기 위해서는 다음과 같은 명령어를 사용해서 접근해야 한다.

• Move from hi (mfhi)

• Move from lo (mflo)

Division

$$Dividend = Quotient * Divisor + Remainder$$

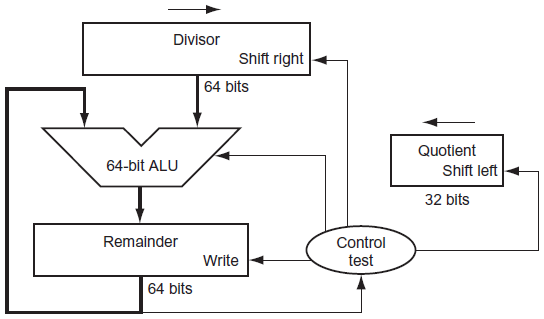
→ $Divisor > Remainder$

Remainder : Hi register에 저장

quotient : Lo register에 저장

→ Multiplier는 오른쪽에서 왼쪽으로 가고, Division은 왼쪽에서 오른쪽으로 감

→ Dividend가 쌓인 것이 Divisor보다 크냐 작나를 판단

Remainder의 초기값을 Dividend로 넣음 (그래서 remainder < divisor)

Divisor를 0010인데, 00100000으로 빼는 이유

: 초기 4개에 대한 몫이 있는지 여부를 판단할 수 있음

→ 만약 signbit가 음수가 되면 못빼는 것

→ 만약 음수가 되면 다시 divisor를 더함 (그러면 원래 값 복구가 될 것이므로)

지속적으로 Divisor를 오른쪽으로 1개 shift시키고 해당 행동을 반복해주면 된다.

(만약 divisor가 4bit면 4번 만큼까지만 오른쪽으로 shift해야함. 안그러면 값을 잃어버림)

→ 그래서 dividor가 32비트인데, divisor가 64비트나 할당하는 것

Faster Division

Problem : Division을 하는데 최대 32 clock 수행해야함.

ALU를 32bit로 줄임 (Input이 32bit일 뿐 output은 64비트가 될 수 있음)

따라서 remainder를 조작함

Remainder의 오른쪽에 dividend를 넣고, 왼쪽에는 0을 채워넣음

→ 그리고 왼쪽 32bit를 ALU에게 계속 주는 것

→ 그리고 계속 dividend가 들어간 영역을 왼쪽으로 1개씩 shift

→ 양수가 될 때까지 계속 왼쪽으로 shift (음수면 사실 ALU에 그대로 주면 되긴함)

→ 빼서 양수가 나와도 비슷한 과정을 반복해주면 됨. (그리고 뺀 결과가 양수가 나오면 가장 오른쪽에 1을 써주면 된다.)

따라서 상위 32비트는 remainder

하위 32비트는 quotient가 저장됨

Floating Point

Fixed point : 소수를 표현하는 위치가 딱 고정됨

Floating point : 변동

Modern PLs support numbers with fractions

컴퓨터 입장에서는 숫자 그대로를 인식하지 못하기 때문에 binary number로 바꿔줘야함.

> Scientific notation

$$1.xxxxxxxx_{(2)} \times 2^{yyyy}$$

dot(.) : binary point

xxxxxxxx : fraction / mantissa

yyyy : exponent

이때, mantissa, exponent를 할당해주는 비트가 변동되는 것이 floating point

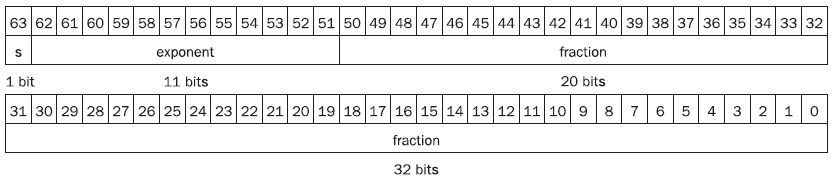
Floating-Point Representation

→ Little endian Format (MSB가 주소가 제일 높은 쪽)

mantissa가 exponent보다 할당되는 bit수가 더 크다.

💡

$(-1)^s\times F \times 2^E$ : 표현하고자 하는 수

Not only overflow, but also underflow can occur

overflow : exponent를 고려해보면 쉽게 발생할 수 있다고 예측 가능. 예를 들어 서로 다른 수를 곱하는 과정에서 exponent field가 표현할 수 있는 범위를 넘을 수 있음

underflow : 사실 음수끼리 곱하는 과정에서 발생하는 것이라 근본적으로 overflow가 발생하는 상황과 대칭적이다.

Single & Double Precision

소수점 아래에 굉장히 많은 숫자들이 많은 경우, 23개의 mantissa로는 불충분함. 이 경우에는 64비트를 사용해야함

→ 이 경우에는 11개의 exponent, 52개의 mantissa field로 사용한다.

→ mantissa쪽에 더 많이 할당하는 것을 볼 수 있음

32비트 : single precision floating point format

64비트 : double precision floating point format

IEEE 754 Standard

32비트, 64비트로 소수를 표현할 때 저장하는 표준을 만든 것

비트가 낭비되는 것을 막기 위해서, leading 1 bit을 implicit

→ 기본적으로 1이라고 가정한다 (1.xxxx)

이러한 가정이 없으면 불필요한 정보를 저장해야함. (1이라고 가정해놓고, 실질적으로 소수 표현할 수 있는 범위를 1개 늘리는 것)

→ Implied 1 + a 23/52-bit fraction

실질적인 값은 significand이고 , leading 1을 제거한 것이 fraction

그래서 실질적인 format은

$$(-1)^S\times(1+Fraction)\times 2^E \\ =(-1)^S\times(1+(s1\times2^{-1}) + (s2\times2^{(-2)} \cdots)\times 2^E$$

Representing Unusual Events

• 왜 무한대같은 개념을 도입했을까?

  Fraction 연산은 exception을 발생시키기에는 overhead가 굉장히 커서, 실수 연산은 exception을 발생시키지 않게끔

Not a Number (NAN) : 0/0, subtraction infinity from infinity

$+\infty, -\infty$ : setting the exponent as the largest value

순서

1. exponent bit이 1인지 판단해야함 (일단 특별한 케이스)
   1. fraction bit이 전부 다 0 : infinity
   2. 0이 아닌 경우 : NaN

Comparison-Friendly Format

사실 주소가 큰 친구부터 비교해보면 대소관계를 쉽게 판단할 수 있음

→ 사실 대소관계에 영향을 끼치는 것은 exponent가 영향이 더 크므로 더 앞에 나오는 것

→ 근데 그러면 exponent field가 음수가 들어오게 되면 번거로워짐

unsigned로 표현하고 bias만큼을 뺌

$$(-1)^S\times (1+Fraction)\times 2^{(Exponent - Bias)}$$

→ 그래야 정수처럼 비교할 때 MSB부터 쭉 내려오면서 하나하나씩 비교할 수 있게 됨

→ 즉 exponent가 표현할 수 있는 범위는 32bit 기준으로 1~ 254로까지로 바뀜 (실제 2의 거듭제곱 위에 올라갈 수 있는 숫자의 범위는 -126 ~ 127

💡

싹 다 0과 싹 다 1은 special meaning

• Bias를 계산하는 방법 (0은 그냥 0임)

  부호 비트는 너무나 당연한 것이므로 넘어가고

  (보통 지수라고 부르는) 자릿수는 8비트이므로 총 256가지를 표현할 수 있지만

  (부호없는 정수형이라고 가정할 때) 최소값인 0은 실제 숫자 0을 표현하기 위해 (뒤에 다시 설명한다.)

  최대값인 255는 무한대 값을 표현하기 위해 예약되어 있다.

  또한 자릿수가 증가하는 방향과(실제 숫자가 큰 경우) 자릿수가 감소하는 방향(실제 숫자가 작은 경우)을

  모두 고려해야 하기 때문에 부호가 필요해지지만, 위에서 정의한 최대/최소값과의 일관적인 표현을 위해

  부호없는 정수형으로 표현하는 것이 좋으므로(?) 실제 값에 일정한 상수를 더해서 저장한다.

  즉, 8비트 중에서 실제로 사용할 수 있는 범위는 1부터 254까지이므로 (총 254개)

  이를 음수/양수로 반반씩 나누어 할당하려면 127을 빼서 -126부터 127까지의 범위를 사용할 수 있고

  저장할 때는 해당하는 수에 127을 더해서 저장하면 된다. (이 때 127은 바이어스 (bias) (상수)라고 한다.)

바꾸는 방법

1. 10진수를 2진수로 돌림

2. exponent에 bias를 더함

Denormalized 형태

32bit 기준으로 실제 2의 승수로 올라갈 수 있는 범위는 -126~127까지이다. 만약 숫자가 정말 작아서

0.124325 x $2^{-126}$ 형태로 표현될 수 밖에 없는 경우

(위 경우 승수를 -127로 만들면 표현할 수 있는 방법이 아얘 존재하지 않는다.)

위 경우를 denormalized로 따로 관리한다.

Exponent : 싹 다 0

mantissa : fraction부분을 그대로 넣는다.

💡

기본적으로 normalized된 형태의 경우 exponent에 기존 승수 + bias만큼이 들어가있는 것과 달리, bias를 더하면 1이 저장되어있어야함에도 불구하고 0으로 저장되어있다. 그냥 가장 낮은 승수(single precision의 경우 -126)를 denormalized가 가지고 있는게 자연스러운 것으로 이해하는 것이 덜 헷갈릴 것이다.

Floating-Point Addition

1. exponent가 큰 쪽에 맞춘다. (조정하는 과정에서 표현 가능한 significand를 초과하는 경우에는 버린다.)

2. significand끼리 더한다.

3. normalized화 시킨다.

4. fraction bit수만큼 rounding시킨다.

Multiplication

1. 새로운 exponent를 계산하고 보정

   → 두 소수의 exponent를 더함

2. significand끼리 곱함

3. normalize

4. fraction bit수만큼 rounding시킨다

5. 부호 처리

MIPS : Floating-Point Support

기존의 레지스터는 정수를 저장하는 목적

그래서 floating point를 저장하는 목적의 register를 따로 관리

(32bit인 register가 32개 존재함)

→ 만약 double precision의 경우 $f0, $f1 이런 방식으로 2개에 걸쳐서 저장함.

만약 add.d $f2, $f4, $f6이라고 적은 경우 f2, f3에 저장하는 것.