[CS231n] Lecture 13

Supervised / Unsupervised Learning

Supervised Learning

1. Label이 존재

2. Label을 통해 loss function을 정의 가능하다.(x -> y로 대응되는 신경망 구축이 가능하다.)

3. Classification, Regression, Object detection, Semantaic segmentation, image captioning이 이에 속함

 

Unsupervised Learning

1. Lbael이 존재하지 않음 (대신, Label이 존재하지 않아서 훈련 비용이 싸다.)

2, Label을 통해 직접적으로 loss function을 정의할 수 없으므로 hidden structure를 이용하게 된다.

3. Clustering, Dimensionality reduction, feature learning, density estimation이 이에 속함

Generative Models

Training data가 주어졌을 때, 동일한/비슷한 분산을 가지는 새로운 샘플을 만들어내는 모델. 접근 방법에 따라서 Explicit한 방법과 Implicit한 방법이 존재한다.

PixelRNN & PixelCNN

$$p(x) = \prod_{i = 1}^n p(x_i|x_1, \cdots , x_{i-1})$$

두 접근법 모두 Explicit하게 density estimation을 다룬다. 위 식에서 볼 수 있는 것처럼 i번째 pixel 값을 결정짓기 위해서는, i - 1번째까지의 pixel이 주어진 상태로 판단해야 한다.추가적으로 곱사건이므로 조건부 확률의 product연산이 된다.

 

매우 Complex distribution이 되므로 이를 해결하기 위해 Neural network를 활용하게 된다.

PixelRNN

RNN을 학습할 때 언급한 것처럼, new state를 결정짓기 위한 식은 다음과 같다

$$h_t = f_W(h_{t - 1}, x_t)$$

위 식에서 볼 수 있는 것처럼, new state를 판단하기 위해서는 old sate을 고려한 상태로 판단하게 된다. 이러한 특성을 활용해서 접근한 것이 PixelRNN이다.

 

다만, RNN의 문제와 동일하게 Sequential하게 판단해야하기 때문에 느리다는 단점을 가지고 있다.

PixelCNN

위 그림에서 볼 수 있는 것처럼, 현재의 pixel값을 판단하기 위해서 이전까지의 pixel까지의 정보를 가지고 CNN을 처리하게 된다.

정확하게는 Masking strategy를 적용하게 되는데, 자세한 메커니즘은 다음과 같다.

왼쪽에 있는 사각형은 input image의 각 pixel값을 의미하고, 노란색은 현재 추정해야하는 pixel의 위치이다.

오른쪽에 있는 사각형은 masking을 하는 pixel으로 추정해야하는 pixel 이전까지를 1, 추정해야하는 pixel과 그 이후 pixel에 대해서는 0으로 maksing처리 하게 된다.

 

따라서 input image에 masking을 처리하게 되면 이전 pixel value까지만 고려할 수 있게 된다.

마찬가지 접근방법을 다음 pixel에 적용하면 다음과 같다.

계속 반복하면 다음과 같다.

Image의 경우 channel을 무시하면 1개의 pixel이 가질 수 있는 값은 0 ~ 255이다.

Trainning input image의 실제 pixel value와 위에서 살펴본 masking stratety를 적용한 CNN의 output value를 softmax loss를 통해 모델을 훈련하게 된다. 직접적인 label은 없지만, input image의 pixel값이 일종의 label로 작용하는 느낌으로 이해할 수 있다.

 

Masking strategy의 각 procedure의 경우 독립적으로 작용하므로, parallel하게 처리해서 속도를 PixelRNN보다 더 끌어올릴 수 있다는 장점이 존재한다.

하지만, 위 그림에서 볼 수 있는 것처럼 Semantic이 Clear하지는 않다는 단점이 존재한다.

Autoencoder

Autoencoder의 경우 훈련 당시에는 input data와 최대한 비슷한 분산을 가지는 reconstructed image를 만드는 것이 목표이다.

이를 원본 iamge와 reconstructed image 사이의 L2 loss를 통해 훈련시킨다.

 

Encoder의 경우 input data를 활용하여 low demension인 z에 매핑시킨다. 이미지에서 중요한 특성을 뽑아내는 과정이므로 demension이 작아진다고 이해해주면 된다.

Decoder의 경우 Encoder의 결과로 나온 z를 활용해 x와 차원이 같고, x와 분산이 비슷한 재구성된 이미지를 output로 출력하게 된다.

 

즉, low dimension으로 만들면서 발생한 정보의 누실을 최대한 완화하고자 하는 방향으로 훈련이 진행되는 것이다.

훈련 후에는 Decoder를 제거한다. 즉, 훈련을 통해 해당 image의 특성을 잘 대변할 수 있는 z를 잘 뽑아내는 Encoder를 확보하게 되는 것이다. 훈련된 Encoder에 input data를 통과시켜서 나온 feature z를 classifier에 주입하고, input data에 해당하는 label과의 차이가 작아지도록 classifier를 훈련시킬 수 있다. 이런 과정을 거치게 되면 data가 부족할 때 유용하게 활용할 수 있게 된다.

 

다만 위 작업의 경우는 new image를 generate하지는 못한다는 단점이 존재한다.

이에 등장한 방법이 Variational Autoencoders이다.

Variational Autoencoders (VAE)

$$p_\theta (x) = \int p_\theta (z) p_\theta (x|z) dz $$

위 식에서 볼 수 있는 것처럼 VAE는 intractable한 density function을 다룬다는 점에서 차이가 있다.

(추가적으로 z가 $\theta$에 대한 확률인 이유는 parameter가 $\theta$ encoder의 output이기 때문으로 이해할 수 있다.)

 

즉, x에 대한 확률이 관측하지 않은 연속형 확률변수 z를 내포하는 식에 의해서 형성된다.

따라서 intractable한 density function을 다뤄야하는 문제가 발생하게 된다.

 

이에 lower bound를 구하고 이를 최적화함으로써 간접적으로 최적화하는 방향으로 진행하게 된다. (즉, 직접적으로 optimize하지는 못한다.)

처음으로 생각할 수 있는 접근 방법은, z가 주어졌을 때 x를 찾는 모델을 훈련하는 것이다. 하지만, 신경망의 output값으로 나온 $p_\theta (x|z)$는 이산적으로만 알아낼 수 있으므로 z의 변화에 따라 적분하는 것이 불가능하다.

$p_\theta (x|z)$를 알 수 없기에 Posterior density도 구할 수 없다. 

 

VAE는 이러한 문제점을 $p(z|x)$에 근사하는 $q(z|x)$를 output으로 가지는 network를 추가로 훈련시킴으로써 해결한다.

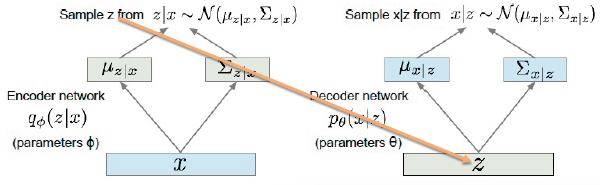
위 사진에서 보는 것처럼, $q(z|x)$가 output인 Encoder의 결과를 활용해 정규분포를 만들고 여기에서 z를 추출하여 Decoder에 넣어주는 과정을 진행하게 된다. 정확한 메커니즘을 수식으로 나타내면 다음과 같다.

맨 처음 식의 경우는 $\text{log}p_\theta (x^{(i)})$가 z에 대해 무관하므로 표현만 수정해준 것이고, 나머지는 베이즈 정리와 로그 성질을 활용해서 정리해준 것이다. (추가적으로 KL divergence에 대해서는 여기에서는 설명을 생략, 자세한 것은 정보이론 참고)

 

수식을 보면, 첫번째 KL divergence의 경우 앞은 encoder의 output, 뒤는 정규분포를 가정한 상태에서 시작했으므로 구할 수 있다.

두번 째 KL divergence의 경우 앞은 Decoder의 output이므로 구할 수 있지만, 뒤는 intractable하다.

 이때, KL divergence는 무조건 0이상이므로 intractable한 부분을 고려하지 않고 구할 수 있는 부분만 묶어서 lower bound를 구한다.

$$ \text{log} p_\theta (x^{(i)}) \geq \mathcal{L}(x^{(i)}, \theta, \phi)$$

$$\theta^*, \phi^* = \text{arg}\max\limits_{\theta, \phi} \sum \limits_{i = 1}^N \mathcal{L}(x^{(i)}, \theta, \phi)$$

 

즉, mini-batch를 돌면서 Lower bound의 값이 최대가 되게끔 하는$\theta$와 $\phi$를 찾는 모델을 trainning하게 되는 것이다.

해당 작업을 가시화하면 다음과 같다.

앞서 살펴본 것처럼 Train 과정에는 encoder와 decoder를 활용해서 두 network를 훈련하게 된다.

Generation procedure의 경우는 Encoder network를 제외하고 Z가 input data가 encoder를 통과한 것을 활용해서 구한 값이 아니라 Gaussian distribution에서 뽑게 된다. 즉 이를 통해 실질적으로 이미지 생성 과정을 거치게 된다.

추가적으로 이미지 생성과정에서 z를 Gaussian distribution에서 뽑기 때문에 각 축은 independent하다. 따라서 각 축이 variation의 해석 가능한 요소로써 이해할 수 있다는 장점이 있다. 그림을 봐도 축을 다고가면서 점진적으로 변화하고 있는 것을 쉽게 파악할 수 있다.

다만, VAE로 만든 이미지의 경우 Blurry하다는 단점이 존재한다.

Generative Adverserial Networks (GAN)

다음 모델은 앞서 살펴본 PixelCNN이나 VAE와 달리 explicitly하게 density를 모델링하지 않고 게임이론을 접목하여  이미지를 generate하게 된다는 점에서 차이점을 가지고 있다.

이를 위해 위 모델은 2가지의 네트워크를 잡고, 해당 네트워크에 게임이론을 접목시켰다.

Generator의 경우는 해당 network의 output이 discriminator network에서 진짜로 인식되게끔 하는 것이 목표이고, Discriminator의 경우는 잔찌와 가짜 이미지를 잘 구분하는 것이 목표이다.

 

설명에서 알 수 있는 것처럼, 두 모델은 일종의 파레토 최적에 이를 수 없는 상황이고 이율배반적이다.

 

이를 수식으로 나타내면 다음과 같다.

$$\min\limits_{\theta_g}\max\limits_{\theta_d}\text{ } [E_{x \sim p_{data}}\text{log}D_{\theta_d}(x) +E_{z \sim p_z}\text{log}(1 - D_{\theta_d}(G_{\theta_g}(z))) ]$$

 

위 식이 크려면 $D_{\theta_d}(x)$가 커여하고 $D_{\theta_d}(G_{\theta_g}(z))$가 작아야 한다. 이를 만족하는 값이 discriminator의 parameter이다.

 

위 식이 작으려면, $D_{\theta_d}(G_{\theta_g}(z))$가 커야 한다. 이를 만족하는 값이 generator의 parameter이다.(단, $D_{\theta_d}(x)$의 경우는 generator의 parameter와 무관하므로 고려하지 않는 것이다.)

이때 generator의 경우 최적점과 멀 때의 상황의 gradient가 flat하고, 반대의 경우가 gradient가 큰 문제점이 발생하게 된다.

따라서 이러한 문제점을 해결하기 위해 gradient descent가 아니라 gradient ascent를 사용하고 min이 아니라 max를 찾아주면 된다.

위 사진처럼 Train 후에는 Random한 noise를 Generator에 주입하게 되면 이미지를 생성하게 된다. 이를 통해 나온 결과는 앞에서 본 다른 모델들보다 많이 좋게 나온다.