[백준 7677번] [분할 정복] Fibonacci

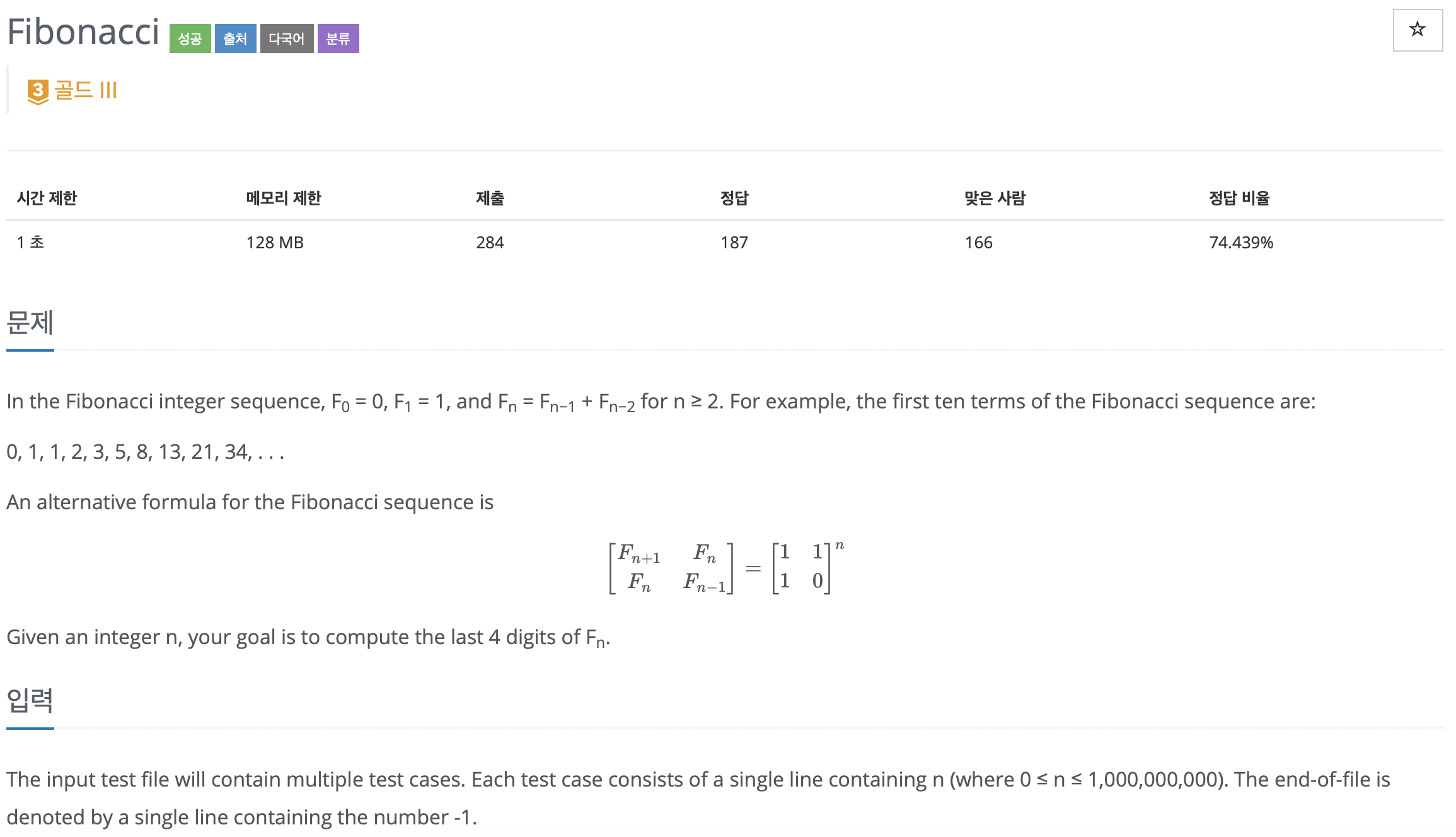
문제 자체는 대표적인 분할정복 예제 중 하나인 거듭수에 대한 계산이다.

그런데 피보나치를 저렇게 나타낼 수 있는 것에 대해서 되게 신기했다.

 

n어 엄청나게 커도 게속해서 절반 쳐주면서 계산하면

O(lgn)으로 처리할 수 있다.

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cmath>
typedef long long ll;

using namespace std;

void fib_set(int n, vector<ll> &dp){
    if(n == 1) {
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 1;
        return;
    }

    if(n % 2 == 0){
        vector<ll> data(4, 0);
        fib_set(n / 2, data);
        dp[0] = (data[0] * data[0] + data[1] * data[2]) % 10000;
        dp[1] = (data[0]* data[1] + data[1] * data[3]) % 10000;
        dp[2] = (data[0] * data[2] + data[2] * data[3]) % 10000;
        dp[3] = (data[1] * data[2] + data[3] * data[3]) % 10000;
        return;
    }
    else{
        vector<ll> data(4, 0);
        fib_set(n / 2, data);
        dp[0] = (data[0] * data[0] + data[1] * (data[0] + data[2] + data[3])) % 10000;
        dp[1] = (data[0] * data[0] + data[1] * data[2]) % 10000;
        dp[2] = (data[3] * data[3] + data[2] * (data[0] + data[1] + data[3])) % 10000;
        dp[3] = (data[2] * (data[0] + data[3])) % 10000;
        return;
    }
}

int main(void){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    while(true){
        int temp;
        cin >> temp;
        if(temp == -1) return 0;
        // 예외처리
        if(temp == 0){
            cout << 0 << "\n";
            continue;
        }
        vector<ll> dp(4, 0);
        fib_set(temp, dp);
        cout << dp[1] << "\n";
    }
}