1. Fundamentals of Computing

What is scientific computing?

Scientific computing concerns with the design and analysis of algorithms for solving mathematical problems that arise in science and engineering

Problem Solving Process

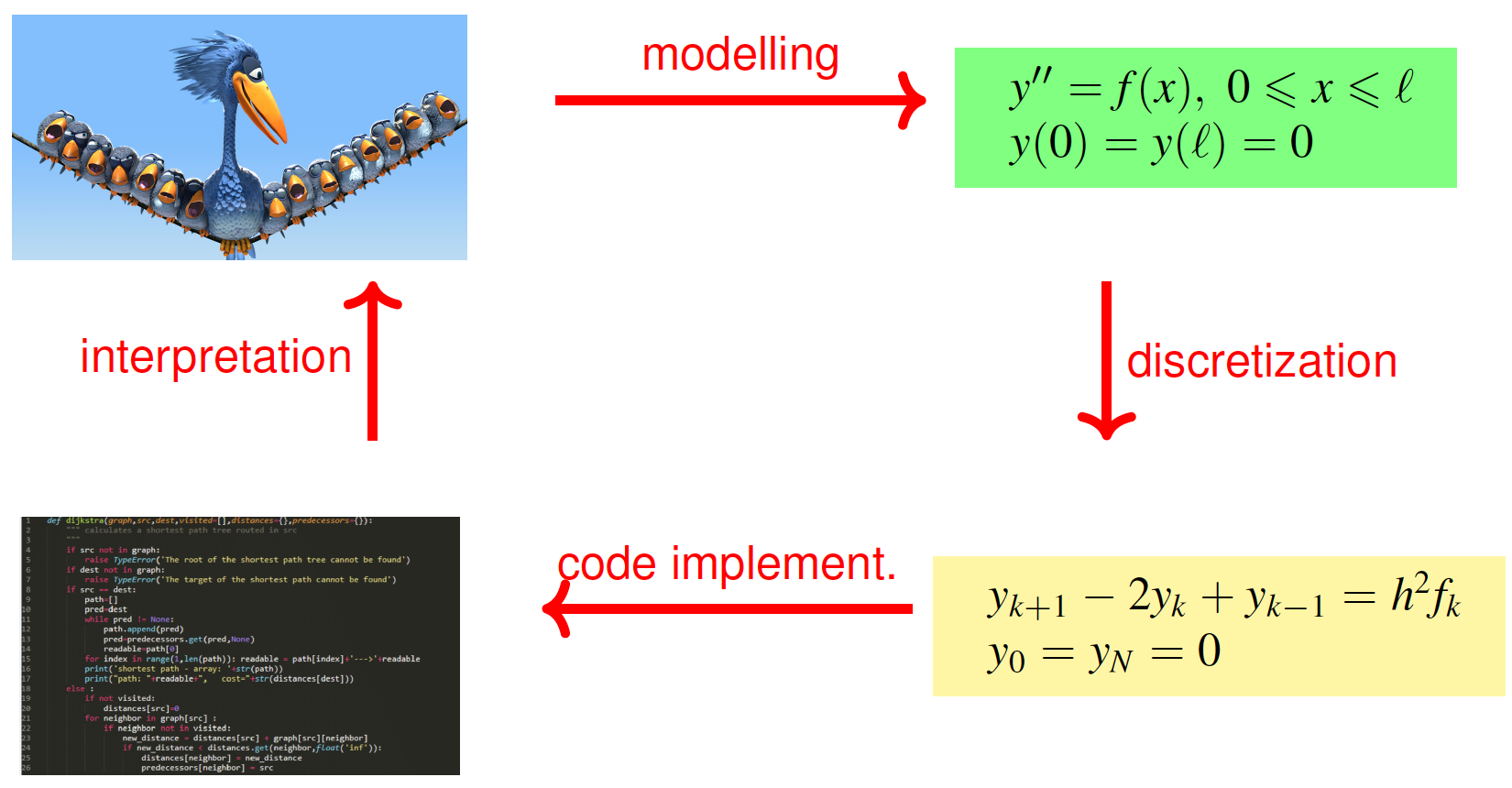
1. Develop a mathematical model

2. Discretize the model and develop algorithms to solve the equations numerically

   💡

   만약 우리가 특정 함수를 taylor 근사를 통해서 접근한다고 했을 때, 특정한 항까지만 고려한 경우 discretize했다고 볼 수 있다. 그래야 컴퓨터를 통해서 계산할 수 있기 때문이다.

3. Implement and execute the algorithms in computer software.

4. Interpret and validate the computed results, repeating any or all of the preceding steps, if necessary

Sources of Approximation

Before computation

1. Mathematical modeling : 즉 모델링 하는 과정에서 근사를 취할 수 있다.

2. Empirical measurements : 즉 데이터 자체 내에 에러가 존재할 수 있다.

3. Previous computations : 이전 결과 자체에서 근사가 있을 수 있다.

During computation

1. Truncation or discretization : 수학적인 근사를 하는 과정에서 발생. 즉 algorithm 자체의 error를 의미한다.

2. Rounding : 컴퓨팅의 한계로 발생하는 error이다.

Others

1. Input의 uncertainty로 인해 문제가 가속화될 수 있다. 이를 conditioning problem 이라고 부른다.

2. input의 perturbation으로 인해 output의 변하는 정도는 모델의 stability와 관련이 있다.

Example

1. Earth is modeled as a sphere, idealizing its true shape (model simplification)

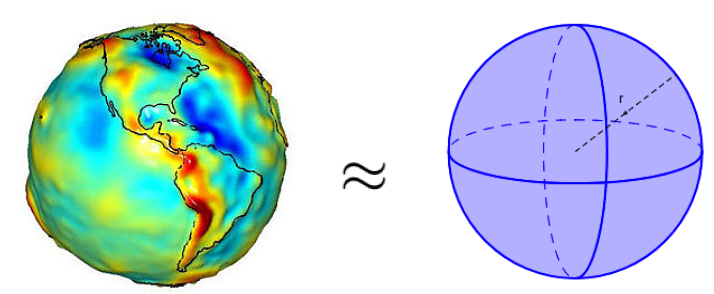
2. Value for radius is based on empirical measurements and previous computations (errors in inputs)

   $$r \approx 6371\text{km}$$

3. Value of $\pi$ requires truncating infinite process (roundoff error)

💡

컴퓨터가 표현할 수 있는 자리수는 한계가 있으므로 이 과정에서 roundoff error가 발생하는 것이다.

4. Values for input data and results of arithmetic operations are rounded by calculator or computer (roundoff error)

   $$A \approx 4 \times 3.14159 \times (6371)^2 \approx 5.10064 \times 10^8 \text{km}^2$$

💡

마찬가지로 컴퓨터가 표현할 수 있는 자리수가 한계가 있기 때문에 roundoff error가 발생하는 것이다.

Truncation Error and Rounding Error

Computation error is the sum of truncation error and rounding error. In addition, one of these usually dominates.

Truncation error

Difference between the true result (for actual input) and the result produced by given algorithm using exact arithmetic

$$f'(x) = \frac{f(x+h) - f(x)}{h} + \frac{Mh}{2}, M = \max|f''(x)|$$

💡

Truncation errors arises when an infinite process is replaced by a finite one

Rounding error

Difference between result produced by given algorithm using exact arithmetic and result produced by the same algorithm using limited precision arithmetic

$$x = \pi, \hat x = 3.141592653189793, \frac{|x - \hat x|}{|x|}\approx 10^{-16}$$

💡

Round-off errors depend on the fact that practically each number in a numerical computation must be rounded(or chopped) to a certain number of digits

Example

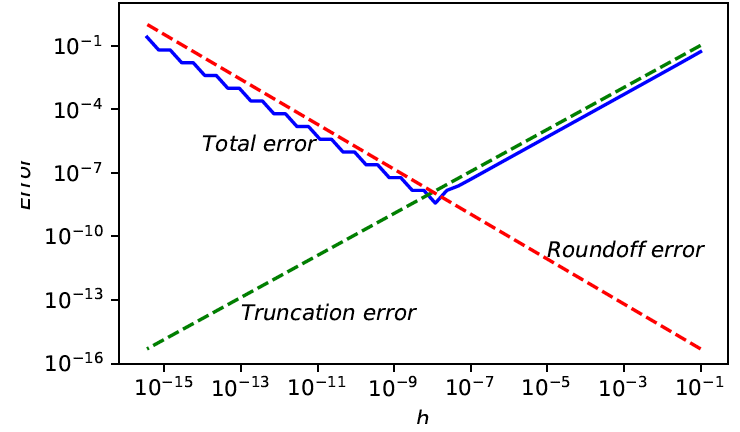
Error in finite difference approximation exhibits tradeoff between rounding error and truncation error

$$f'(x) \approx \frac{f(x+h) - f(x)}{h}$$

1. Truncation error bounded by $Mh/2$

2. Rounding error bounded by $2\epsilon /h$, where error in function values bounded by $\epsilon$

3. Total error minimized when $h \approx 2\sqrt{\epsilon/M}$

   💡

   증명은 간단히 산술기하를 활용해주면 된다.

   → Error increases for smaller $h$ because of rounding error and increases for larger $h$ because of truncation error

Absolute Error and Relative Error

Absolute error

Approximate value - true value

$$\|x - \hat x\|$$

Relative error

$$\frac{\text{absolute error}}{\text{true value}} = \frac{\|x - \hat x\|}{\|x\|}$$

It is equivalent to

$$\text{approx value}= \text{(true value)}\times \text{(1 + rel error)}$$

💡

True value는 실제로는 알 수 없는 것이므로, estimate error 를 구하거나 bound error 를 구한다.

Floating-Point Numbers

Floating-point number system characterized by four integers

$$\beta : \text{base or radix} \\ p : precision \\ \left[ L, U\right]: \text{exponent range}$$

→ 따라서 Floating-point number system은 다음과 같이 표기될 수 있다.

$$\mathbb F(\beta, p, L, U)$$

예를 들어 $x \in \R$는 다음과 같이 표현된다.

$$\begin{aligned} x &= (-1)^\sigma(d_0.d_1d_2\cdots d_{p - 1})_\beta \times \beta^e \\ &= (-1)^\sigma(d_0 + d_1\beta^{-1} + d_2\beta^{-2}+\cdots + d_{p - 1}\beta^{-(p - 1)})\times \beta^e \end{aligned}$$

where digits $d_k \in \{0, 1, \dots, \beta - 1\}$ with $d_0 \ne 0$ (for normalization) and exponent $e$ is an integer such that

$$L \le e \le U$$

💡

2진법 기준으로 $d_0 \ne 0$을 보장해줌으로써 추가적인 bit를 사용하지 않아도 된다는 장점이 존재하게 된다. (해당 bit를 mantissa에 더 사용할 수 있다.)

Properties

1. Total number of normalized floating-point numbers is

   $$2(\beta - 1)\beta^{p - 1}(U - L + 1) + 1$$

2. Smallest positive normalized number

   $$x_{\min} = \beta^L$$

3. Largest floating-point number

   $$x_{\max} = \beta^{U + 1}(1 - \beta^{-p})$$

   💡

   제일 작은 숫자 단위가 $\beta^{-(p - 1)}$이다. 1은 $\beta^U$에 붙었다고 생각해주면 된다. 해당 숫자를 더해주게 되면 $\beta^{U + 1}$이 되면서 자릿수가 증가하기 때문에, 저 숫자가 최대라고 할 수 있다.

4. Floating-point numbers equally spaced only between successive powers of $\beta$

   💡

   당연히 단위는 $\beta^e$만큼 동간격으로 떨어지게 된다.

5. Not all real numbers are exactly representable; those that are called machine numbers

   💡

   앞에서 설명한 것처럼 컴퓨터는 bit의 한계 때문에 round-off를 반드시 수행해야 한다. 이 과정을 통해 나타낼 수 있는 숫자들을 machine number 라고 하는 것이다.

6. Numbers in $\mathbb F$ are symmetric with respect to zero

   💡

   Computer Architecture에서 배운 것처럼 sign-bit를 차용하기 때문이라고 이해하면 될 듯 싶다.

Example

💡

위 그림에서 확인할 수 있는 것처럼, 숫자가 커질수록 absolute-error는 커지게 된다. 하지만 true-value가 커짐에 따라서 relative-error는 작아지게 된다. 이에 수치 계산에서 더 일관된 정밀도를 유지할 수 있게 되는 장점이 존재한다.

Machine Epsilon

Definition

The distance between 1 and the smallest machine number larger than 1 is called machine epsilon and is denoted with $\epsilon_M$. The value of machine epsilon is

$$\epsilon_M = \beta^{-(p - 1)}$$

💡

제일 작은 숫자의 단위이다. 또한 추가적으로 이러한 소리를 하려면 $L$이 적어도 0이하의 수를 가진다는 것이 전제되어야 한다. 사실상 $\epsilon_M = \text{ulp}(1) = \epsilon_M\beta^0$으로 연관지어서 이해할 수 있다.

Definition

The distance between any machine number $x \in \mathbb F$ and its consecutive machine number(successor) is called unit in the last place and is denoted with $\text{ulp}(x)$

$$\text{ulp}(x) = \beta^{-(p - 1)}\times \beta^e = \beta^{e-p+1} = \epsilon_M\beta^e$$

💡

$\beta^e$는 현재 $x$에 대응되는 exponent값을 그대로 가져왔다고 생각해주면 된다. 즉, ulp의 중요한 점은 successor와의 거리를 machine epsilon을 활용해서 표현할 수 있다는 것이다.

Hidden Bit

Today’s computers use base 2 to internally represent numbers. Therefore, the only choice of digits that remains for the leading bit $d_0$ is $d_0 = 1$. This creates an opportunity to save some memory if we avoid occupying the bit $d_0$ with the fixed value of 1. This implicit bit whose value is always 1 for any normalized binary number is called the hidden bit.

$$\begin{aligned} x &= \pm (1.d_1d_2\cdots d_{p - 1})_\beta \times \beta^e \\ &= \pm(1 + d_1\beta^{-1} + d_2\beta^{-2} + \cdots + d_{p - 1}\beta^{-(p - 1)})\times \beta ^e\end{aligned}$$

Rounding Rules

If real number $x$ is not exactly representable, then it is approximated by nearby floating-point number $\text{fl}(x)$:

$$\text{fl}(x) : \R \to \mathbb F(\beta,p, L, U)$$

This process is called rounding, and error introduced is called rounding error or rondoff error

Rounding rules

Assume $x = \pm (d_0.d_1\cdots d_{p - 1}d_p \cdots)_\beta \times \beta^e$

Chopping

Truncate base-$\beta$ expansion of $x$ after $(p - 1)$-st digit

$$\text{fl}(x) = \pm (d_0.d_1\cdots d_{p - 1})_\beta \times \beta^e$$

💡

단순 버림을 진행한 것이라고 생각해주면 된다.

$$\frac{|\text{fl}(x) - x|}{|x|}\le \frac{\epsilon_M \beta^e}{(d_0.d_1d_2\cdots)_\beta\beta^e} \le \frac{\epsilon_M}{(1.0)_\beta} = \epsilon_M$$

Rounding to nearest

$\text{fl}(x)$ is the nearest floating-point number to $x$, using floating-point number whose last stored digit is even in case of tie

$$\text{fl}(x) = \pm (d_0.d_1\cdots d_{p - 2}\tilde d_{p - 1})_\beta \times \beta^e,$$

where $\tilde d_{p - 1}$ is either $d_{p - 1}$ or $d_{p - 1} + 1$

💡

반올림과 유사하나, 단 5인 경우에는 결과가 짝수가 되게끔한다는 점에서 차이를 보인다.

💡

Rounding to nearest는 가장 정확하기 때문에 기본값으로 설정된다.

$$\frac{|\text{fl}(x) - x|}{|x|}\le \frac{\epsilon_M}{2}$$

Unit roundoff

Definition

The smallest number $\delta$ such that $\text{fl}(1 + \delta) > 1$ is called unit roundoff and is denoted by $u$, that is

$$u = \begin{cases}\frac{\epsilon_M}{2}, &\text{if rounding is used} \\ \epsilon_M, & \text{if chopping is used}\end{cases}$$

💡

$\epsilon_M$은 1의 successor까지의 거리인데 rounding을 사용하게 되면 절반만 가면 된다.

For either chopping or rounding to the nearest we have

$$\frac{|\text{fl}(x) - x|}{|x|}\le u$$

which is equivalent to

$$\text{fl}(x) = x(1+\delta),$$

where $|\delta|\le u$

Subnormal numbers

A relatively large gap between zero and $x_{\min}$ (underflow region)

Therefore, we define the concept of subnormal numbers as follows

$$x= \pm (0.d_1d_2\cdots d_{p - 1})_\beta \times \beta^L$$

💡

정수부가 0이라는 점과 exponent가 $L$이라는 점을 주의해야 한다.

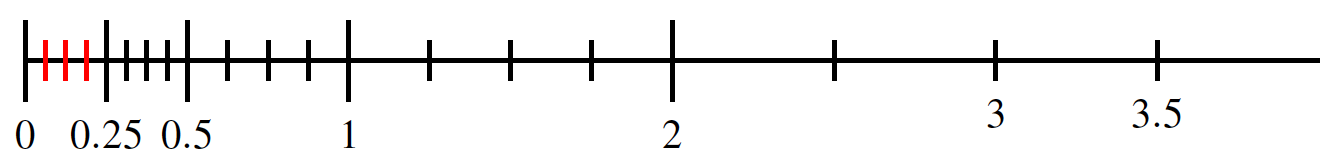
Gradual underflow

Let $\text{fl}(x) = \pm (0.0\cdots0 d_{p - k}\cdots d_{p - 1})_\beta \times \beta^L$ with $d_{p - k}\ne 0$ then

$$\begin{aligned}\frac{|\text{fl}(x) - x|}{|x|}&\le \frac{1}{2}\frac{\beta^{L - (p - 1)}}{(0.0\cdots010\cdots0)_\beta \times \beta^L} \\&= \frac{1}{2}\frac{\beta^{-(p - 1)}}{\beta^{-(p - k)}} \\ &= \frac{1}{2}\beta^{-k + 1}\end{aligned}$$