12. Expectation Maximization

Gaussian Mixture Model (GMM)

현재 주어진 label이 없는 training set $\{x^{(1)}, \dots, x^{(n)}\}$의 distribution을 추정하고 싶다. 이를 위해서 다음과 같은 joint distribution을 모델링한다.

$$p(x^{(i)}, z^{(i)}) = p(x^{(i)}|z^{(i)})p(z^{(i)})$$

이때, $z^{(i)} \sim \text{Multinomial}(\phi)$ and $x^{(i)}|z^{(i)} \sim \mathcal N(\mu_j, \Sigma_j)$이고, multinomial은 총 $k$개의 원소가 존재한다. (이때, k는 hyper-parameter이다.)

💡

Variational Inference에서도 설명했지만 $z^{(i)}$는 latent random variable로 distribution을 구성하는데는 관여하지만 직접적으로 관측되지는 않는 변수를 의미한다.

따라서 위 model에서의 parameter는 $\mu, \phi, \Sigma$이다.

💡

k-mean clustering algorithm과 유사한 측면이 있다. isotropy한 gaussian을 적용한 특정한 사례라고 할 수 있다.

그렇다면 “기존의 방식처럼 Likelihood를 정의하고, 이를 최대로 하는 parameter를 찾는 식으로 해결할 수는 없을까?”라는 의문을 가질 수 있다. 이에 대한 답을 알아보기 위해서, Likelihood를 살펴보도록 하자.

$$\mathcal l(\phi, \mu, \Sigma) = \sum_{i = 1}^n\log p(x^{(i)};\phi, \mu, \Sigma) \\ = \sum_{i = 1}^n\log p(x^{(i)}|z^{(i)};\phi, \mu, \Sigma)p(z^{(i)};\phi, \mu, \Sigma) \\ = \sum_{i = 1}^n\log p(x^{(i)}|z^{(i)};\phi, \mu, \Sigma)p(z^{(i)};\phi)$$

(맨 마지막 식에서, $z^{(i)}$는 $\phi$에만 dependent하기 때문에 나머지 parameter를 지워도 무방하다)

최적의 parameter를 구하기 위하여 likelihood를 각각의 parameter에 대해서 미분하고 0이 되는 지점을 찾으려 해보면, 결과적으로 해당 식을 만족하는 closed form 형태가 존재하기 않는다는 것을 발견할 수 있게 된다. 즉 기존의 방식처럼 단순히 구할 수 없다.

예를 들어 다음과 같은 상황을 생각해보도록 하자.

1. $k = 2$이고 각 정규분포는 표준편차가 1이다.

2. 또한 각 정규분포의 평균은 각각 $\mu, \mu+2$이다.

3. latent prior는 각각 $\pi_1, \pi_2$이다 ($\pi_1 + \pi_2 = 1)$

$x = 3$인 데이터가 주어졌다고 가정했을 때 MLE는 다음과 같다.

$$\argmax_\mu \pi_1\frac{1}{\sqrt{2\pi}}\exp(-\frac{(3-\mu)^2}{2}) + \pi_2{\sqrt{2\pi}}\exp(-\frac{(1-\mu)^2}{2})$$

이거의 최댓값을 구하기 위해서는 numerical한 방법밖에 없다. 실제 계산을 해보면 다음과 같다.

💡

즉 GMM에서는 직접적으로 MLE를 적용하기 어렵다.

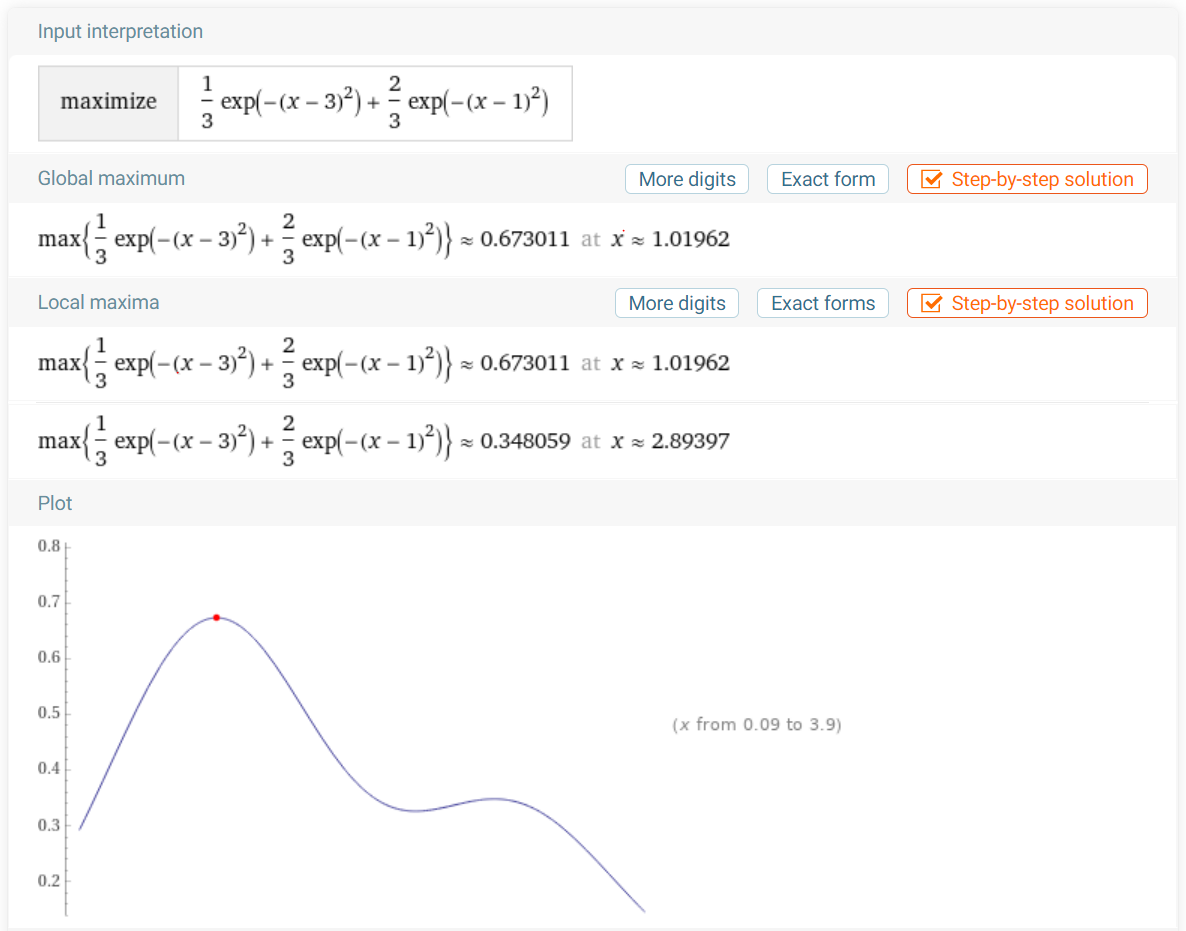
앞서 살펴본 것처럼 MLE를 통해 likelihood를 최대로 하는 parameter를 직접적으로 계산하기가 어렵다. 이를 해결하기 위해서는 EM algorithm 을 적용해야 한다. 하지만 EM algorithm을 알아보기에 앞서, 그보다 상위 범주인 Variational inference에 대해서 알아보도록 하자.

Variational Inference

Goal

The goal of variational inference is to find a variational distribution that is close to the true posterior distribution. This is done by iteratively updating the parameters of the variational distribution until the Kullback-Leibler divergence between the variational distribution and the posterior distribution is minimized.

Motivation

다음과 같은 joint distribution을 생각해보자. latent variable $\bold z = z_{1:m}$ 이고 observation $\bold x = x_{1:n}$

$$p(z, x) = p(z)p(x|z)$$

기본적으로 Bayesian model에서는 latent variable은 data의 distribution을 찾는데 사용이 된다. 기본적인 아이디어는 다음과 같다.

1. Latent variable $\bold z$는 prior density function $p(\bold z)$를 따른다.

2. 해당 latent variable를 이용하여 observation과 관련을 짓는다. $p(\bold x |\bold z)$

   💡

   MoG의 경우에는 latent variable을 이용해서 likelihood가 Gaussian을 따른다고 가정함으로써 observation과 관련을 짓게 된다.

3. 이를 통해 결과적으로 추론하고 싶은 것은 $p(\bold z | \bold x)$ 즉 posterior이다. 이를 Inference problem이라고 부른다.

   💡

   즉 variational model은 generative model이다. 결과적으로 최종 목표는 data의 distribution을 추론하고자 하는 것이다.

해당 $p(\bold z|\bold x)$를 구하면 무엇을 할 수 있을까? 크게 보면 다음과 같은 작업을 수행할 수 있게 된다.

1. Latent variable에 대한 point estimate or interval estimate

2. new data에 대한 predictive density

구하고자 하는 $p(\bold z | \bold x)$를 알기 위해서는 다음과 같은 정보를 알아야 한다.

$$p(\bold z | \bold x) = \frac{p(\bold z, \bold x)}{p(\bold x)}$$

이때, $p(\bold x)$를 Evidence라고 부르고 다음과 같은 방법으로 구할 수 있다.

$$p(\bold x) = \int p(\bold z, \bold x) d\bold z$$

하지만, 대부분의 model에서 해당 적분은 closed form 으로 구하는 것이 불가능하거나, 계산 과정에서 시간 복잡도가 exponential이 되는 문제점을 가지고 있다.

💡

이러한 측면에서 Generative model이 Discriminative model보다 더 복잡하다고 하는 것이다. 모델이 복잡해질수록 evidence를 intractable하게 되기 때문이다.

Variational Inference

Variational Bayesian methods

Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usually termed "data") as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes:

https://en.wikipedia.org/wiki/Variational_Bayesian_methods

Expectation Maximization (EM)

The EM algorithm is an iterative method for finding the maximum likelihood (ML) or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step.

💡

즉 latent variable가 있는 MLE나 MAP estimates를 하는데 EM algorithm이 굉장히 강력하게 사용된다.

E-step

Tries to get soft guess for the values of the $z^{(i)}$’s, denoted by $w_j^{(i)}$

$$w_j^{(i)}:=p(z^{(i)} = j|x^{(i)};\phi, \mu, \Sigma) \\ = \frac{p(x^{(i)}|z^{(i)} = j;\phi, \mu, \Sigma)p(z^{(i)} = j|\phi)}{\sum_{l = 1}^kp(x^{(i)}|z^{(i)} = l;\phi, \mu, \Sigma)p(z^{(i)} = l|\phi)}$$

💡

$w_j^{(i)}$ 는 각 data $i$가 j번째 gaussian으로부터 나왔을 확률을 의미한다.

M-step

Updates the parameters of the model based on previous guesses. Pretending that the guesses in the first part were correct

$$\phi_j := \frac{1}{n}\sum_{i = 1}^nw_j^{(i)} \\ \mu_j := \frac{\sum_{i = 1}^nw_j^{(i)}x^{(i)}}{\sum_{i = 1}^nw_j^{(i)}} \\ \Sigma_j := \frac{\sum_{i = 1}^nw_j^{(i)}(x^{(i)} - \mu_j)(x^{(i)}-\mu_j)^T}{\sum_{i = 1}^nw_j^{(i)}}$$

💡

사실 위 식은 $w_j^{(i)}$를 $\mathbb{1}\{z^{(i)} = j\}$로 바꾸면 각 data가 어느 gaussian에 속하는지 미리 아는 상태에서 MLE를 통해 parameter update하는 것과 완벽하게 동일하다.

Relevence with K-means cluster

K-means algorithm의 경우, k cluster 들 중 1개로 hard cluster를 진행시켰다. 예를 들어 A, B cluster가 존재하고 해당 cluster의 centroid와의 거리가 거의 유사해도 더 가까운 cluster에 할당했다. 이를 hard assignment 라고 한다.

반면 EM algorithm의 경우는 soft assignment 를 진행하게 된다. 이러한 점에서 차이를 보인다고 할 수 있다.

또한 K-means algorithm과 EM algorithm은 local optima에 영향을 많이 받는다는 공통점이 존재한다. 즉, 다른 initial parameter를 설정함에 따라 결과가 달라질 수 있으므로, 여러 초기값을 설정해보는 것이 좋다.

So it is actually converges?

지금까지 GMM에서 EM algorithm을 통해 최적의 parameter를 iterative하게 구하는 방법에 대해서 다뤘다. 하지만, 어떻게 해당 식이 유도가 되었고, 반드시 수렴하는지 여부에 대해서 고찰해볼 필요가 존재한다.

먼저 일반적인 Expectation Maximization은 무엇인지 살펴보기 전에 Jensen’s Inequality에 대해서 알아보도록 하자.

Jensen’s Inequality

Convex set

A set $C \sub \R^d$ is convex if

$$\lambda x + (1-\lambda)y \in C, \forall x, y\in C \text{ and }\forall \lambda \in [0, 1]$$

Convex function

For a convex set $C \sub \R^d$, a function $f:C \to \R$ is convex if

$$f(\lambda x + (1-\lambda)y) \le \lambda f(x)+(1-\lambda)f(y), \forall x, y\in C \text{ and } \forall \lambda\in [0, 1]$$

💡

$f''(x) \ge 0 , \forall x\in \R$ means $f$ is convex function

만약 $f$가 vector-valued input인 경우에는 hessian $H$가 positive semi-definite($H \ge 0)$이면 된다.

💡

$f''(x) > 0, \forall x\in \R$ means $f$ is a strictly convex function

Jensen’s Inequality for random variables

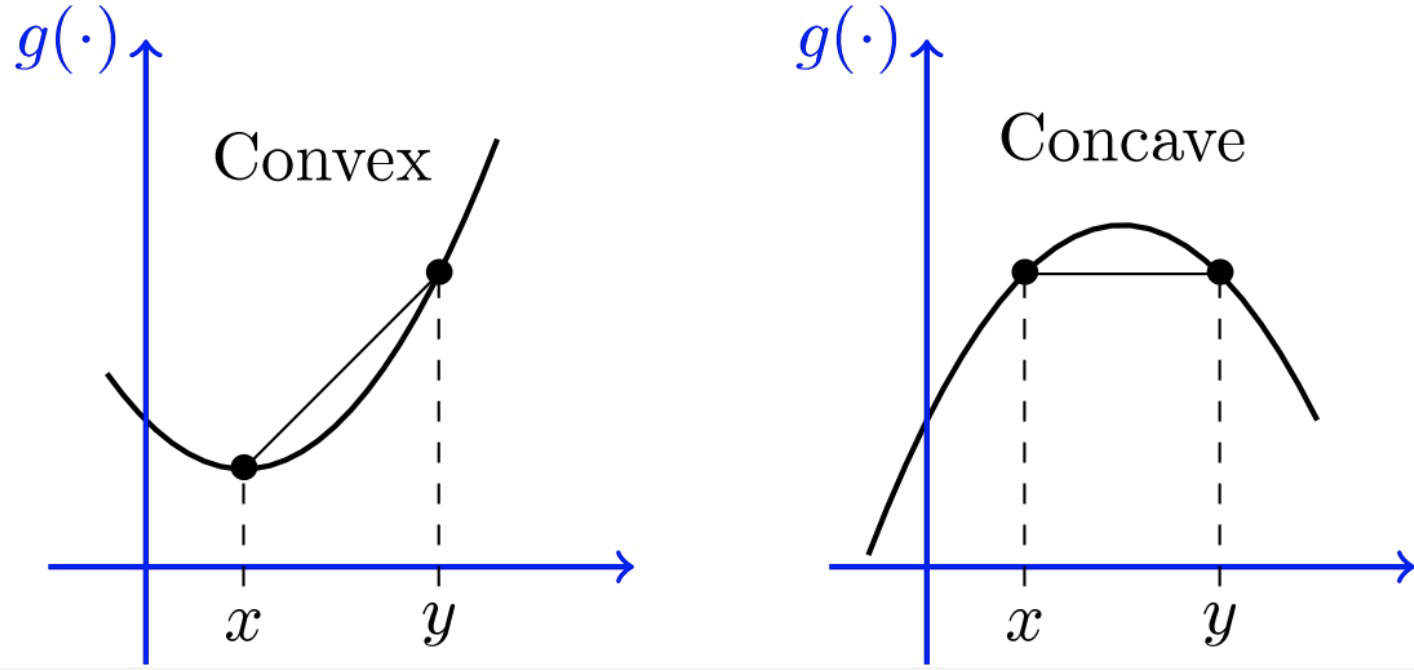
For a convex set $C$, if function $f:C\to \R$ is convex and $X$ is a random vector on $C$, then

$$E[f(X)] \ge f(E[X])$$

In the case of a concave function $f$, we have

$$E[f(x)] \le f(E[x])$$

💡

If $f$ is strictly convex, $E[f(X)] = f(E[X]) \Leftrightarrow X \text{ is a constant}$ (정확하게는 probability 1으로 같다)

증명은 Recursive 하게 증명해주면 된다.

💡

Concave function의 경우에는, 앞에서 정의한 것들의 부호를 전부 다 바꿔주면 된다.

General EM Algorithm

Suppose we have an estimation problem in which we have a training set $\{x^{(1)}, \dots, x^{(n)}\}$ consisting of $n$ independent examples. We have a latent variable model $p(x, z; \theta)$ with $z$ being the latent variable.

💡

Estimation problem typically refers to the task of inferring unknown quantities or parameters based on observed data. The goal is to find the best estimate or approximation for these unknowns. 즉 $\theta$를 추정하고 싶은 것

$p(x;\theta)$를 구하기 위해서는 모든 latent variable인 $z$에 대해서 marginalization을 해주면 된다.

$$p(x;\theta) = \sum_zp(x, z;\theta)$$

이때 log-likelihood를 다음과 같이 정의한다.

$$\mathcal l(\theta) = \sum_{i = 1}^n \log p(x^{(i)};\theta) \\ = \sum_{i = 1}^n \log\sum_zp(x, z;\theta) \\$$

log-likelihood가 최대가 되게끔 하는 $\theta$를 추정하는 방식으로 최적화를 진행하게 된다.

$$\argmax_\theta \mathcal l(\theta)$$

하지만 위 식이 최대가 되게끔 하는 $\theta$를 analytic(closed-form)하게 찾는 것은 굉장히 어렵다. 왜냐하면 결과적으로 굉장히 어려운 non-convex optimization problem을 풀게 되기 때문이다.

따라서 EM algorithm을 통해서 maximum-likelihood를 만족하는 $\theta$를numerically하게 추정하려고 시도하게 된다. 이때 EM algorithm은 iterative algorithm으로 다음과 같은 image로 이해하면 된다.

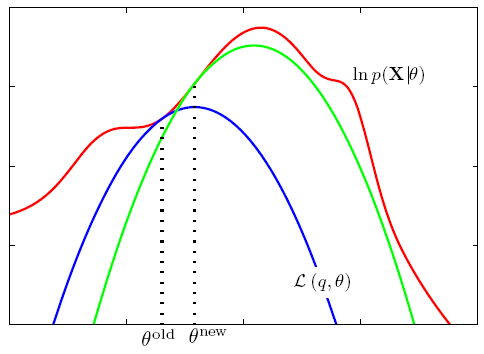
EM-algorithm은 대략 다음과 같은 과정을 거쳐서 진행되게 된다.

1. E-step에서는 $l(\theta)$의 lower-bound를 construct한다. 이때 해당 lower-bound는 2가지의 특성을 가진다.
   1. 모든 $\theta$에 대해서 $l(\theta)$보다 더 작다.
   2. $\theta_{old}$에 대해서는 $l(\theta)$와 값이 같다.

2. M-step에서는 E-step에서 구한 lower-bound를 기준으로 maximum이 되게끔하는 $\theta_{new}$를 찾는다.

3. $\theta_{new}$를 사용해서 1 과정을 반복한다.

💡

EM-algorithm은 local optimum에 수렴하게 된다. 즉 초기 시작점에 따라 global optimum을 발견하지 못할 수 있다.

위 상황에서 $Q_i$를 도입해서 문제 상황을 다시 정의해보도록 하자.

💡

이때, $Q_i$는 $z^{(i)}$이 가질 수 있는 값에 대한 distribution으로 $\sum_{z^{(i)}}Q_i(z^{(i)}) = 1$ 이다.

$$l(\theta) = \sum_{i = 1}^n\log\sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta) \\ = \sum_{i = 1}^n\log\sum_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

이때, $z^{(i)}$가 probability distribution $Q_i$로 부터 온 것이므로 위 식을 다시 변형할 수 있게 된다.

$$\sum_{i = 1}^n\log\sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta) \\ = \sum_{i = 1}^n\log\sum_{z^{(i)}}Q_i(z^{(i)})\biggr [ \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \biggr ]\\= \sum_{i = 1}^n\log\mathbb E_{z^{(i)}\sim Q_i}\biggr [ \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \biggr ]$$

위 식에 Jensen's Inequality 를 적용해주면 다음과 같다.

$$\sum_{i = 1}^n\log\mathbb E_{z^{(i)}\sim Q_i}\biggr [ \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \biggr ] \ge \sum_{i = 1}^n\mathbb E_{z^{(i)}\sim Q_i}\log\biggr [ \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \biggr ]$$

💡

$\log$ 함수가 concave이므로 Jensen’s Inequality를 적용할 수 있다.

이때, Jensen’s Inequality를 통해 구한 값을 다시 풀어쓰면 다음과 같다.

$$\sum_{i = 1}^n\mathbb E_{z^{(i)}\sim Q_i}\log\biggr [ \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \biggr ] = \sum_{i = 1}^n \sum_{z^{(i)}} Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

즉 위 결과를 통해

$$l(\theta) \ge \sum_{i = 1}^n \sum_{z^{(i)}} Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

임을 알 수 있다. 이때, 앞서 그림으로 살펴본 것처럼 lower bound를 구할 때 현재 $\theta$에 대해서는 값이 같아야한다. 그래야 lower bound에서의 최적의 $\theta$를 찾아나가는 과정이 $l(\theta)$에서도 최적이라고 말할 수 있기 때문이다.

추가적으로 논의의 편의를 위해

$$ELBO(x^{(i)};Q_i, \theta) := \sum_{z^{(i)}} Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\ ELBO(Q, \theta) := \sum_{i = 1}^n \sum_{z^{(i)}} Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = \sum_{i = 1}^n ELBO(x^{(i)};Q_i, \theta)$$

💡

즉, Jensen’s Inequality 상에서 등식이 성립하게끔 하는 $Q_i(z^{(i)})$를 찾는 것이 목표이다. (당연히 $Q_i(z^{(i)})$를 어떻게 잡느냐에 따라 lower-bound가 달라진다.)

앞서 논의한 것처럼 Jensen’s Inequality에서 등식이 성립하기 위해서는

$$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = \text{constant}$$

이어야 한다. 즉, 어떤 $z^{(i)}$를 선택하든 위 값이 같아야하는 것이다.

즉,

$$Q_i(z^{(i)}) \propto p(x^{(i)},z^{(i)};\theta)$$

이때

$$\sum_{z^{(i)}}Q_i(z^{(i)}) = 1 \\ \Rightarrow Q_i(z^{(i)}) = \frac{p(x^{(i)}, z^{(i)};\theta)}{\sum_{z^{(i)}}p(x^{(i)}, z^{(i)};\theta)} = p(z^{(i)}|x^{(i)};\theta)$$

💡

즉, $Q_i(z^{(i)})$를 $p(z^{(i)}|x^{(i)};\theta)$로 잡음으로써 log-likelihood의 lower-bound를 tight하게 만들 수 있다.

여태까지의 논의를 정리하면 다음과 같다.

E-step

Set $Q_i(z^{(i)}) = p(z^{(i)}|x^{(i)};\theta)$

M-step

Find $\theta$ s.t

$$\theta:= \argmax_\theta \sum_{i = 1}^n\sum_{z^{(i)}}Q_i(z^{(i)})\log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

💡

여기서는 $Q_i(z^{(i)})$를 고정한다.

💡

추가적으로 mixture of gaussian의 경우에는 $z^{(i)}$가 discrete하지만, factor analysis에서는 continuous하다. 따라서 factor analysis의 경우 sigma가 아니라 integration을 취해주게 된다.

Mixture of Gaussians revisited

위 상황에서

$$p(x^{(i)}|z^{(i)} = j; \phi, \mu, \Sigma) = \frac{1}{(2\pi)^{d/2}|\Sigma_{j}|^{1/2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{j})^T{\Sigma_{j}}^{-1}(x^{(i)}-\mu_{j})) \\ x^{(i)}|z^{(i)} = j \sim \mathcal N(\mu_j, \Sigma_j)$$

$$p(z^{(i)} = j) = \phi_j \\ z^{(i)}\sim \text{Multinomial}(\phi)$$

(이때 $z^{(i)}$는 $1, \dots, k$ 까지의 값을 가질 수 있다. 즉 k개의 Gaussian이 있다고 생각하면 된다.)

Likelihood가 최대가 되게끔하는 $\phi, \mu, \Sigma$를 찾는 것이 목표이다. 앞서 논의한 것처럼

$$\argmax_{\phi, \mu, \Sigma} \sum_{i = 1}^n\log \sum_{z^{(i)} = 1}^kp(x^{i}|z^{(i)} = k;\phi, \mu, \Sigma)$$

를 analytical하게 구하는 것은 힘들다.

💡

$\log$ 안쪽으로 Gaussian이 더해져있는 형태이므로 딱 봐도 closed form 형태가 나올 수 없다. 추가적으로 GDA의 경우에는 label로 인해서 어느 gaussian에 속하는지는 결정되어서 $\log$ 안에 Gaussian이 더해져 있는 꼴이 나오지 않는는 점을 비교해서 정리해야 한다.

따라서 EM-Algorithm을 활용해서 Numerically 하게 구하고자 하는 것이다.

앞서 언급한 것처럼

$$w_i^j :=Q_i(z^{(i)} = j) = p(z^{(i)} = j|x^{(i)};\phi,\mu, \Sigma)$$

를 만족하는 $Q_i$ distribution을 잡으면 주어진 $\phi, \mu, \Sigma$ 에 대해서 $l(\phi,\mu, \Sigma)$와 접점을 가진다.

💡

즉 $ELBO( Q_i, \phi, \mu, \Sigma) = l(\phi,\mu, \Sigma)$ 를 주어진 $\phi, \mu, \Sigma$ 에 대해서 만족한다.

그리고 M-step에서는 위 $ELBO( Q_i, \phi, \mu, \Sigma)$를 가지고 최대가 되게끔하는 $\phi, \mu, \Sigma$를 구한다.

$$\max_{\phi, \mu, \Sigma} \sum_{i = 1}^n\sum_{j = 1}^k w_j^{(i)}\log\frac{\frac{1}{(2\pi)^{d/2}|\Sigma_{j}|^{1/2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{j})^T{\Sigma_{j}}^{-1}(x^{(i)}-\mu_{j}))*\phi_j}{w_j^{(i)}}$$

위 식을 각 parameter에 대해서 미분하고 해당 값이 0이 되는 parameter를 구해주면 된다.

$$\nabla_{\mu_l}\sum_{i = 1}^n\sum_{j = 1}^k w_j^{(i)}\log\frac{\frac{1}{(2\pi)^{d/2}|\Sigma_{j}|^{1/2}}exp(-\frac{1}{2}(x^{(i)}-\mu_{j})^T{\Sigma_{j}}^{-1}(x^{(i)}-\mu_{j}))*\phi_j}{w_j^{(i)}} \\ = -\nabla_{\mu_l}\sum_{i = 1}^n\sum_{j = 1}^k w_j^{(i)}\frac{1}{2}(x^{(i)}-\mu_{j})^T{\Sigma_{j}}^{-1}(x^{(i)}-\mu_{j}) \\ = \frac{1}{2}\sum_{i = 1}^nw_l^{(i)}\nabla_{\mu_l}2\mu_l^T\Sigma_l^{-1}x^{(i)} - \mu_l^T\Sigma_l^{-1}\mu_l \\ = \sum_{i = 1}^n w_l^{(i)}(\Sigma_l^{-1}x^{(i)} -\Sigma_l^{-1}\mu_l) = 0$$

💡

주의해야할 지점은 $w_l^{(i)}$는 여기서는 고정된 값이다. 즉 상수 취급한다는 점을 주의해야 한다.

Therefore

$$\mu_l := \frac{\sum_{i = 1}^nw_l^{(i)}x^{(i)}}{\sum_{i = 1}^nw_l^{(i)}}$$

💡

이때, $w_l^{(i)}$ 는 $x^{(i)}$가 Gaussian $l$에 속하는 정도를 보정해준 것이라고 이해해주면 된다. 정확히는 $p(z^{(i)}= l|x^{(i)}; \phi, \mu, \Sigma)$

비슷한 과정으로 진행한 결과는 다음과 같다

$$\phi_j := \frac{1}{n}\sum_{i = 1}^nw_j^{(i)} \\ \mu_j := \frac{\sum_{i = 1}^nw_j^{(i)}x^{(i)}}{\sum_{i = 1}^nw_j^{(i)}} \\ \Sigma_j := \frac{\sum_{i = 1}^nw_j^{(i)}(x^{(i)} - \mu_j)(x^{(i)}-\mu_j)^T}{\sum_{i = 1}^nw_j^{(i)}}$$

💡

$\phi_j$를 구하기 위해서는 Lagransian을 활용해야하는데, 해당 내용은 CS229 Lecture note를 참고하도록 하자.

Convergence of EM algorithm

앞서 살펴본 것처럼

$$l(\theta) \ge ELBO(Q, \theta)\text{ for all } \theta, Q$$

E-Step : Maximize $ELBO(Q, \theta)$ with respect to $Q$

M-Step : Maximize $ELBO(Q, \theta)$ with respect to $\theta$

💡

즉 EM algorithm은 coordinate ascent 라고 이해할 수도 있다.

그러면 EM-algorithm이 결과적으로 local maximum에 converge할 것임을 증명해보도록 하자.

Suppose $\theta^{(t)}$ and $\theta^{(t+1)}$ are the parameters from successive iterations of EM.

So it is enough to show that

$$l(\theta^{(t)})\le l(\theta^{(t+1)})$$

(This shows that EM always monotonically improves log-likelihood)

In E-step, we choose $Q_i$ such that

$$Q_i^{(t)} = p(z^{(i)}|x^{(i)};\theta) \\ \Rightarrow l(\theta^{(t)}) = ELBO(Q_i, \theta^{(t)})$$

In M-step, we update the $\theta$ so that

$$ELBO(Q_i^{(t)},\theta^{(t)}) \le ELBO(Q_i^{(t)}, \theta^{(t+1)})$$

Since, $ELBO(Q_i^{(t)}, \theta^{(t+1)})$ is still a lower-bound of $l$ so

$$ELBO(Q_i^{(t)}, \theta^{(t+1)}) \le l(\theta^{(t+1)})$$

Therefore

$$l(\theta^{(t)}) \le l(\theta^{(t+1)})$$